
【题目】计算:
(1)14+24﹣8
(2)(﹣3)﹣(﹣2)+(﹣4)
(3)﹣23÷![]() ×(﹣
×(﹣![]() )2
)2
(4)(![]() +
+![]() ﹣
﹣![]() )×(﹣36)
)×(﹣36)
(5)﹣14﹣![]() ×[2﹣(﹣3)2]
×[2﹣(﹣3)2]
【答案】(1)30;(2)﹣5;(3)﹣8;(4)﹣27;(5)![]()
【解析】
(1)根据有理数的加减法运算法则进行计算即可;(2)根据负数的加减运算法则进行计算即可;(3)根据有理数的运算法则先算乘方再算乘除法;(4)根据分式的运算法则,先算括号里的,再算乘法;(4)先算乘方,再算括号内的,再算乘法,最后算减法.
解:(1)14+24﹣8
=14+24+(﹣8)
=30;
(2)(﹣3)﹣(﹣2)+(﹣4)
=(﹣3)+2+(﹣4)
=﹣5;
(3)﹣23÷![]() ×(﹣
×(﹣![]() )2
)2
=﹣8×![]()
=﹣8;
(4)(![]() +
+![]() ﹣
﹣![]() )×(﹣36)
)×(﹣36)
=(﹣18)+(﹣30)+21
=﹣27;
(5)﹣14﹣![]() ×[2﹣(﹣3)2]
×[2﹣(﹣3)2]
=﹣1﹣![]() ×[2﹣9]
×[2﹣9]
=﹣1﹣![]() ×(﹣7)
×(﹣7)
=﹣1+![]()
=![]() .
.


科目:初中数学 来源: 题型:
【题目】矩形OABC有两边在坐标轴的正半轴上,如图所示,双曲线y= ![]() 与边AB、BC分别交于D、E两点,OE交双曲线y=
与边AB、BC分别交于D、E两点,OE交双曲线y= ![]() 于点G,若DG∥OA,OA=3,则CE的长为( )
于点G,若DG∥OA,OA=3,则CE的长为( ) 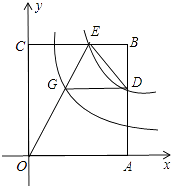
A.![]()
B.1.5
C.![]()
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个. 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2+bx的图象过点A(﹣1,3),顶点B的横坐标为1.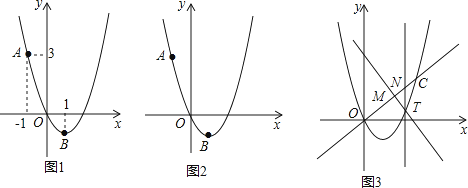
(1)求这个二次函数的表达式;
(2)点P在该二次函数的图象上,点Q在x轴上,若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;
(3)如图3,一次函数y=kx(k>0)的图象与该二次函数的图象交于O、C两点,点T为该二次函数图象上位于直线OC下方的动点,过点T作直线TM⊥OC,垂足为点M,且M在线段OC上(不与O、C重合),过点T作直线TN∥y轴交OC于点N.若在点T运动的过程中, ![]() 为常数,试确定k的值.
为常数,试确定k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.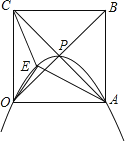
(1)建立适当的平面直角坐标系,
①直接写出O、P、A三点坐标;
②求抛物线L的解析式;
(2)求△OAE与△OCE面积之和的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象的一支位于第一象限.
的图象的一支位于第一象限.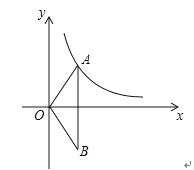
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com