
【题目】某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( ) 
A.
B.
C.
D.
【答案】A
【解析】解:S△AEF= ![]() AE×AF=
AE×AF= ![]() x2 , S△DEG=
x2 , S△DEG= ![]() DG×DE=
DG×DE= ![]() ×1×(3﹣x)=
×1×(3﹣x)= ![]() ,
,
S五边形EFBCG=S正方形ABCD﹣S△AEF﹣S△DEG=9﹣ ![]() x2﹣
x2﹣ ![]() =﹣
=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,
,
则y=4×(﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() )=﹣2x2+2x+30,
)=﹣2x2+2x+30,
∵AE<AD,
∴x<3,
综上可得:y=﹣2x2+2x+30(0<x<3).
故选:A
先求出△AEF和△DEG的面积,然后可得到五边形EFBCG的面积,继而可得y与x的函数关系式.本题考查了动点问题的函数图象,解答本题的关键是求出y与x的函数关系式,对于有些题目可以不用求出函数关系式,根据走势或者特殊点的值进行判断.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( ) 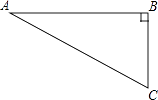
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F. 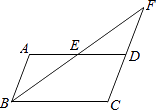
(1)证明:FD=AB;
(2)当ABCD的面积为8时,求△FED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b(a≠0)的图形与反比例函数y= ![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2). 
(1)求该反比例函数和一次函数的解析式.
(2)求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:
①abc>0
②4a+2b+c>0
③4ac﹣b2<8a
④ ![]() <a<
<a< ![]()
⑤b>c.
其中含所有正确结论的选项是( )
A.①③
B.①③④
C.②④⑤
D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本中有一个例题:
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2 .
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题:
(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)14+24﹣8
(2)(﹣3)﹣(﹣2)+(﹣4)
(3)﹣23÷![]() ×(﹣
×(﹣![]() )2
)2
(4)(![]() +
+![]() ﹣
﹣![]() )×(﹣36)
)×(﹣36)
(5)﹣14﹣![]() ×[2﹣(﹣3)2]
×[2﹣(﹣3)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A.7:20
B.7:30
C.7:45
D.7:50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于不等式组  下列说法正确的是( )
下列说法正确的是( )
A.此不等式组无解
B.此不等式组有7个整数解
C.此不等式组的负整数解是﹣3,﹣2,﹣1
D.此不等式组的解集是﹣ ![]() <x≤2
<x≤2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com