
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A.7:20
B.7:30
C.7:45
D.7:50
【答案】A
【解析】∵开机加热时每分钟上升10℃,∴从30℃到100℃需要7分钟.
设一次函数关系式为:y=k1x+b,将(0,30),(7,100)代入y=k1x+b得k1=10,b=30. ∴y=10x+30(0≤x≤7).
令y=50,解得x=2.
设反比例函数关系式为:![]() ,将(7,100)代入
,将(7,100)代入![]() 得k=700,∴
得k=700,∴![]() 。
。
将y=30代入![]() ,解得
,解得![]() ,∴
,∴![]() (7≤x≤
(7≤x≤![]() ).
).
令y=50,解得x=14.
∴饮水机的一个循环周期为![]() 分钟.每一个循环周期内,在0≤x≤2及14≤x≤
分钟.每一个循环周期内,在0≤x≤2及14≤x≤![]() 时间段内,水温不超过50℃.
时间段内,水温不超过50℃.
逐一分析如下:
选项A:7:20至8:45之间有85分钟.85﹣![]() ×3=15,位于14≤x≤
×3=15,位于14≤x≤![]() 时间段内,故可行;
时间段内,故可行;
选项B:7:30至8:45之间有75分钟.75﹣![]() ×3=5,不在0≤x≤2及14≤x≤
×3=5,不在0≤x≤2及14≤x≤![]() 时间段内,故不可行;
时间段内,故不可行;
选项C:7:45至8:45之间有60分钟.60﹣![]() ×2=
×2=![]() ≈13.3,不在0≤x≤2及14≤x≤
≈13.3,不在0≤x≤2及14≤x≤![]() 时间段内,故不可行;
时间段内,故不可行;
选项D:7:50至8:45之间有55分钟.55﹣![]() ×2=
×2=![]() ≈8.3,不在0≤x≤2及14≤x≤
≈8.3,不在0≤x≤2及14≤x≤![]() 时间段内,故不可行.
时间段内,故不可行.
综上所述,四个选项中,唯有7:20符合题意. 故选A.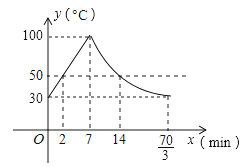 .
.


科目:初中数学 来源: 题型:
【题目】小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离. 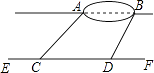
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.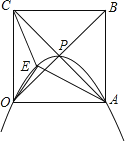
(1)建立适当的平面直角坐标系,
①直接写出O、P、A三点坐标;
②求抛物线L的解析式;
(2)求△OAE与△OCE面积之和的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为AB=|a﹣b|,回答下列问题:
(1)数轴上表示1和﹣3的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点分别是点A和B,如果AB=2,那么x= ;
(3)互不相等的有理数a,b,c在数轴上的对应点分别为A,B,C,如果|c﹣a|+|b﹣c|=|a﹣b|,那么,在点A,B,C中居中的点是 .
(4)当|x+2|+|x﹣1|取最小值时,相应的x的取值范围是 .
若|x﹣a|+|x﹣b|的最小值为4,若a=3,则b的值为 .
式子|x﹣1|+|x﹣2|+|x﹣3|+…+|x﹣617|的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象的一支位于第一象限.
的图象的一支位于第一象限.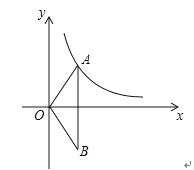
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )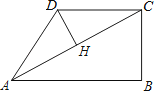
A.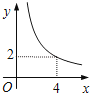
B.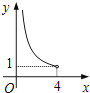
C.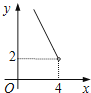
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年二十国集团领导人峰会(简称“G20峰会”)于9月4日至5日在浙江杭州召开,为保证会议期间交通畅通,杭州市已发布9月1日至7日为“G20峰会”调休期间.据报道对于杭州市民:浙江省旅游局联合11个市开展一系列旅游惠民活动,活动内容为:“本省游”、“黄山游”、“黔东南游”,某旅游公司为了解群众出游情况,拟采用分层抽样的方法从有意愿“本省游”、“黄山游”、“黔东南游”这三个区域旅游的群众中抽取7人进行某项调查,已知有意愿参加“本省游”、“黄山游”、“黔东南游”的群众分别有360,540,360人.
(1)求从“本省游”、“黄山游”、“黔东南游”,三个区域旅游的群众分别抽取的人数;
(2)若从抽得的7人中随机抽取2人进行调查,用列举法计算这2人中至少有1人有意愿参加“本省游”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com