
【题目】点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为AB=|a﹣b|,回答下列问题:
(1)数轴上表示1和﹣3的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点分别是点A和B,如果AB=2,那么x= ;
(3)互不相等的有理数a,b,c在数轴上的对应点分别为A,B,C,如果|c﹣a|+|b﹣c|=|a﹣b|,那么,在点A,B,C中居中的点是 .
(4)当|x+2|+|x﹣1|取最小值时,相应的x的取值范围是 .
若|x﹣a|+|x﹣b|的最小值为4,若a=3,则b的值为 .
式子|x﹣1|+|x﹣2|+|x﹣3|+…+|x﹣617|的最小值是 .
【答案】(1)4;(2)1或﹣3;(3)C;(4)﹣2≤x≤1,7或﹣1,95172.
【解析】
(1)根据数轴上两点间的距离的表示方法分别解答即可;(2)根据两点间的距离的表示方法列式,再根据绝对值的性质求解即可;(3)根据|c-a|是A、C间的距离,|b-c|是B、C间的距离,|a-b|是A、B间的距离.即可求解;(4)①当|x+2|+|x-1|取最小值时,有![]() ,求解即可;②根据线段上的点到线段两端点的距离的和最小,分为b在a的左侧和b在a的右侧两种情况求解;③在数轴上找出表示x的点,使它到表示1,617各点的距离之和最小,代入x的值求和即可.
,求解即可;②根据线段上的点到线段两端点的距离的和最小,分为b在a的左侧和b在a的右侧两种情况求解;③在数轴上找出表示x的点,使它到表示1,617各点的距离之和最小,代入x的值求和即可.
解:(1)|1﹣(﹣3)|=4,
故答案为:4;
(2)AB=|x﹣(﹣1)|=|x+1|=2,解得:x=1,x=﹣3;
故答案为:1或﹣3;
(3)|c﹣a|是A,C间的距离,|b﹣c|是B,C间的距离,|a﹣b|是A,B间的距离.
∵|a﹣c|+|b﹣c|=|a﹣b|,
∴点A,B,C中居中的点是点C,
故答案为:C;
(4)①当代数式|x+2|+|x﹣1|取最小值时,相应的x的取值范围﹣2≤x≤1;
②由线段上的点到线段两端点的距离的和最小,
当点b在a的右侧时,
得P在3点与b点的线段上,|x﹣3|+|x﹣b|的值最小为4,
|x﹣3|+|x﹣b|最小=x﹣3+b﹣x=4,
解得:b=7;
当点b在a的左侧时,
得P在3点与b点的线段上,|x﹣3|+|x﹣b|的值最小为4,
|x﹣3|+|x﹣b|最小=3﹣x+x﹣b=4,
解得:b=﹣1;
③根据绝对值的几何意义,求|x﹣1|+|x﹣2|+|x﹣3|+…+|x﹣617|的最小值
就是在数轴上找出表示x的点,使它到表示1,2,,617各点的距离之和最小,当x=309时,原式的值最小,
最小值是308+307+…+1+1+2+…+308=95172.故答案为:﹣2≤x≤1,7或﹣1,95172.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】课本中有一个例题:
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2 .
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题:
(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.
(1)b= , c= , 点B的坐标为;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A.7:20
B.7:30
C.7:45
D.7:50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 与
与![]() 是反比例函数
是反比例函数![]() 图象上的两个点.
图象上的两个点.
(1)求m和k的值
(2)若点C(-1,0),连结AC,BC,求△ABC的面积
(3)根据图象直接写出一次函数的值大于反比例函数的值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b和反比例函数y= ![]() 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( ) 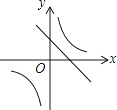
A.
B.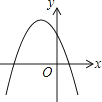
C.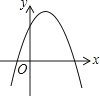
D.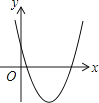
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:(要求保留作图痕迹,不写作法)

(1)作△ABC中BC边上的垂直平分线EF(交AC于点E,交BC于点F);
(2)连结BE,若AC=10,AB=6,求△ABE的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com