搜索
【题目】一次函数y=ax+b和反比例函数y= 
在同一平面直角坐标系中的图象如图所示，则二次函数y=ax2+bx+c的图象大致为（ ）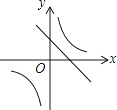 
A.
B.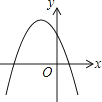
C.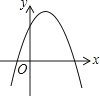
D.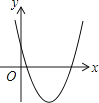
参考答案：
【答案】C
【解析】解：∵一次函数y=ax+b经过一、二、四象限，
∴a＜0，b＞0，
∵反比例函数y= 
的图象在一、三象限，
∴c＞0，
∵a＜0，
∴二次函数y=ax2+bx+c的图象的开口向下，
∵b＞0，
∴ 
＞0，
∵c＞0，
∴与y轴的正半轴相交，
故选C．
【考点精析】根据题目的已知条件，利用一次函数的图象和性质和反比例函数的图象的相关知识可以得到问题的答案，需要掌握一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远；反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，二次函数y=ax2+bx的图象过点A（﹣1，3），顶点B的横坐标为1．
（1）求这个二次函数的表达式；
（2）点P在该二次函数的图象上，点Q在x轴上，若以A、B、P、Q为顶点的四边形是平行四边形，求点P的坐标；
（3）如图3，一次函数y=kx（k＞0）的图象与该二次函数的图象交于O、C两点，点T为该二次函数图象上位于直线OC下方的动点，过点T作直线TM⊥OC，垂足为点M，且M在线段OC上（不与O、C重合），过点T作直线TN∥y轴交OC于点N．若在点T运动的过程中，
为常数，试确定k的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，抛物线y=﹣
x2+ 
x+3与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，抛物线的顶点为点E．
（1）判断△ABC的形状，并说明理由；
（2）经过B，C两点的直线交抛物线的对称轴于点D，点P为直线BC上方抛物线上的一动点，当△PCD的面积最大时，Q从点P出发，先沿适当的路径运动到抛物线的对称轴上点M处，再沿垂直于抛物线对称轴的方向运动到y轴上的点N处，最后沿适当的路径运动到点A处停止．当点Q的运动路径最短时，求点N的坐标及点Q经过的最短路径的长；
（3）如图2，平移抛物线，使抛物线的顶点E在射线AE上移动，点E平移后的对应点为点E′，点A的对应点为点A′，将△AOC绕点O顺时针旋转至△A1OC1的位置，点A，C的对应点分别为点A1 ， C1 ， 且点A1恰好落在AC上，连接C1A′，C1E′，△A′C1E′是否能为等腰三角形？若能，请求出所有符合条件的点E′的坐标；若不能，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】某校校园内有一个大正方形花坛，如图甲所示，它由四个边长为3米的小正方形组成，且每个小正方形的种植方案相同．其中的一个小正方形ABCD如图乙所示，DG=1米，AE=AF=x米，在五边形EFBCG区域上种植花卉，则大正方形花坛种植花卉的面积y与x的函数图象大致是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知a≥2，m2﹣2am+2=0，n2﹣2an+2=0，则（m﹣1）2+（n﹣1）2的最小值是（ ）
A.6
B.3
C.﹣3
D.0 -
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）14+24﹣8
（2）（﹣3）﹣（﹣2）+（﹣4）
（3）﹣23÷
×（﹣
）2（4）（
+
﹣
）×（﹣36）（5）﹣14﹣
×[2﹣（﹣3）2] -
科目： 来源： 题型：
查看答案和解析>>【题目】一次函数y=ax+b（a≠0）与二次函数y=ax2+bx+c（a≠0）在同一平面直角坐标系中的图象可能是（ ）
A.
B.
C.
D.
相关试题
