
【题目】已知![]() 与
与![]() 是反比例函数
是反比例函数![]() 图象上的两个点.
图象上的两个点.
(1)求m和k的值
(2)若点C(-1,0),连结AC,BC,求△ABC的面积
(3)根据图象直接写出一次函数的值大于反比例函数的值的![]() 的取值范围.
的取值范围.
【答案】(1)∵![]() 与
与![]() 是反比例函数
是反比例函数![]() 图象上的两个点,
图象上的两个点,
∴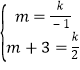 ,解得
,解得![]() .
.
∴![]() .
.
(2)由(1)得,A的坐标是(-1,-2),B的坐标是(2,1),
设直线AB的解析式是y=ax+b,则![]() ,解得:
,解得:![]() .
.
∴直线AB的解析式是y=x-1.
当y=0时,x=1,即OD=1.
∵C(-1,0),∴CD=2.
∴△ABC的面积是![]() ×2×1+
×2×1+![]() ×2×2=3.
×2×2=3.
(3)一次函数的值大于反比例函数的值的x的取值范围是-1<x<0或x>2.
【解析】
(1)把A、B的坐标代入反比例函数解析式得出方程组,求出即可;
(2)求出A、B坐标,求出直线AB,求出直线AB和x轴交点坐标,根据三角形面积公式求出即可;
(3)根据A、B坐标结合图象求出即可.
【考点精析】本题主要考查了确定一次函数的表达式和反比例函数的图象的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点才能正确解答此题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b和反比例函数y= ![]() 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( ) 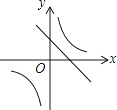
A.
B.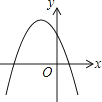
C.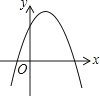
D.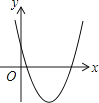
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点P(3a,a)是反比例函数y=![]() (k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
A.y=![]()
B.y=![]()
C.y=![]()
D.y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为AB=|a﹣b|,回答下列问题:
(1)数轴上表示1和﹣3的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点分别是点A和B,如果AB=2,那么x= ;
(3)互不相等的有理数a,b,c在数轴上的对应点分别为A,B,C,如果|c﹣a|+|b﹣c|=|a﹣b|,那么,在点A,B,C中居中的点是 .
(4)当|x+2|+|x﹣1|取最小值时,相应的x的取值范围是 .
若|x﹣a|+|x﹣b|的最小值为4,若a=3,则b的值为 .
式子|x﹣1|+|x﹣2|+|x﹣3|+…+|x﹣617|的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据卫生防疫部门要求,游泳池必须定期换水,清洗.某游泳池周五早上8:00打开排水孔开始排水,排水孔的排水速度保持不变,期间因清洗游泳池需要暂停排水,游泳池的水在11:30全部排完.游泳池内的水量Q(m2)和开始排水后的时间t(h)之间的函数图象如图所示,根据图象解答下列问题: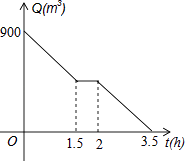
(1)暂停排水需要多少时间?排水孔排水速度是多少?
(2)当2≤t≤3.5时,求Q关于t的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A、C在坐标轴上,点P在BC边上,直线l1:y=2x+3,直线l2:y=2x﹣3.
(1)分别求直线l1与x轴,直线l2与AB的交点坐标;
(2)已知点M在第一象限,且是直线l2上的点,若△APM是等腰直角三角形,求点M的坐标;
(3)我们把直线l1和直线l2上的点所组成的图形为图形F.已知矩形ANPQ的顶点N在图形F上,Q是坐标平面内的点,且N点的横坐标为x,请直接写出x的取值范围(不用说明理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com