
 如图,正方形ABCD的边长为8,点M在边DC上,且DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( )
如图,正方形ABCD的边长为8,点M在边DC上,且DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( )| A. | 8 | B. | 8$\sqrt{2}$ | C. | 2$\sqrt{17}$ | D. | 10 |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
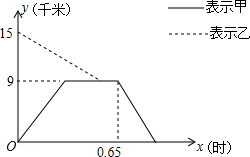 乙骑摩托车与B城相距15千米的A城办事,为了节省时间,甲同时从A城开车出发,先到达C城的D处,并在C城用了12分钟加油回到D处,此时乙已经到达D处等候甲3分钟了,乙把摩托车放到D处,乘甲开的汽车去A城,他们与A城的距离y千米与时间x之间的关系如图,回答下列问题:
乙骑摩托车与B城相距15千米的A城办事,为了节省时间,甲同时从A城开车出发,先到达C城的D处,并在C城用了12分钟加油回到D处,此时乙已经到达D处等候甲3分钟了,乙把摩托车放到D处,乘甲开的汽车去A城,他们与A城的距离y千米与时间x之间的关系如图,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
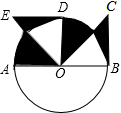 如图,AB是⊙O的直径,过点B作BC⊥OB,且BC=OB,点C在AB的上方,连接OC,△OBC绕着点O逆时针旋转90°得到△ODE
如图,AB是⊙O的直径,过点B作BC⊥OB,且BC=OB,点C在AB的上方,连接OC,△OBC绕着点O逆时针旋转90°得到△ODE查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com