
已知点A(x1,y1),B(x2,y2)在二次函数y=x2+mx+n的图象上,当x1=1,x2=3时,y1=y2.
(1)①求m的值;②若抛物线与x轴只有一个公共点,求n的值;
(2)若P(a,b1),Q(3,b2)是函数图象上的两点,且b1>b2,求实数a的取值范围.
【考点】抛物线与x轴的交点;二次函数图象上点的坐标特征.
【专题】计算题.
【分析】(1)①利用当x1=1,x2=3时函数值相等得到1+m+n=9+3m+n,然后解关于m的方程即可得到m的值;
②根据△=b2﹣4ac=0时,抛物线与x轴有1个交点得到16﹣4n=0,然后解关于n的方程即可;
(2)讨论:当P(a,b1),Q(3,b2)在对称轴的右侧,利用二次函数的性质易得a>3时,b1>b2;当P(a,b1),Q(3,b2)在对称轴的两侧,通过比较两点到对称轴的距离的大小可判断a<1时,b1>b2.
【解答】解:(1)①∵x1=1,x2=3时,y1=y2,
∴1+m+n=9+3m+n,
∴m=﹣4;
②∵抛物线与x轴只有一个公共点,
∴△=m2﹣4n=0,即16﹣4n=0,
∴n=4;
(2)∵抛物线的对称轴为直线x=1,
∴当P(a,b1),Q(3,b2)在对称轴的右侧,则a>3时,b1>b2;
当P(a,b1),Q(3,b2)在对称轴的两侧,而当x1=1,x2=3时,y1=y2,则a<1时,b1>b2.
∴实数a的取值范围为a<1或a>3.
【点评】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2﹣4ac决定抛物线与x轴的交点个数:△=b2﹣4ac>0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.也考查了分类讨论思想的运用.


科目:初中数学 来源: 题型:
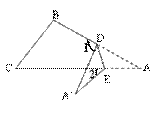
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则 与
与 和
和 之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
A. B.
B.
C. D.
D.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
氢原子中电子和原子核之间的距离为0.00000000529厘米,用科学记数法表示这个距离为( )
A.5.29×10-8 cm B.5.29×10-9cm
C.0.529×10-8 cm D.52.9×10-10 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
对于函数y= - ,下列结论错误的是 ( )
,下列结论错误的是 ( )
A、当x>0时,y随x的增大而增大
B、当x<0时,y随x的增大而增大
C、当x=1时的函数值大于x= -1时的函数值
D、在函数图象所在的象限内,y随x的增大而增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com