如图①,在Rt△AOB中,∠AOB=90°,AB=5,cosA=
.一动点P从点O出发,以每秒1个单位长度的速度沿OB方向匀速运动;另一动点Q从点B出发,以每秒1个单位长度的速度沿BO方向匀速运动.两动点同时出发,当第一次相遇时即停止运动.在点P、Q运动的过程中,以PQ为一边作正方形PQMN,使正方形PQMN和△AOB在线段OB的同侧.设运动时间为t(单位:秒).

(1)求OA和OB的长度;
(2)在点P、Q运动的过程中,设正方形PQMN和△AOB重叠部分的面积为S,请直接写出S与t之间的函数关系式以及相应的自变量t的取值范围;
(3)如图②,现以△AOB的直角边OB为x轴,顶点O为原点建立平面直角坐标系xOy.取OB的中点C,将过点A、C、B的抛物线记为抛物线T.
①求抛物线T的函数解析式;
②设抛物线T的顶点为点D.在点P、Q运动的过程中,设正方形PQMN的对角线PM、QN交于点E,连接DE、DN.是否存在这样的t,使得△DEN是以EN、DE为两腰或以EN、DN为两腰的等腰三角形?若存在,请求出对应的t的值;若不存在,请说明理由.


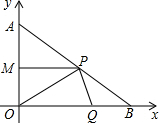 分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)
分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)