
【题目】如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,求GF的长. 
【答案】解:∵正方形ABCD,
∴∠A=∠B=90°,∠AEG+∠AGE=90°,
∵∠GEF=90°,
∴∠AEG+∠BEF=90°,
∴∠AGE=∠BEF,
∴△AEG∽△BFE,
∵E为AB边的中点,
∴GA:AE=BE:BF,
∴AE=BE= ![]() ,GE=
,GE= ![]() ,EF=
,EF= ![]() ,GF=
,GF= ![]() =3.
=3.
另法:取GF的中点H,连接EH,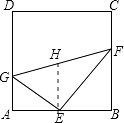
∵GA∥BF,GF和BA不平行,
∴四边形GABF是梯形,
∴EH= ![]() (梯形中位线定理),
(梯形中位线定理),
∵GA=1,BF=2,
∴EH= ![]() ,
,
∵∠GEF=90°,
∴△GEF是直角三角形,
∴GF=2EH=2× ![]() =3(直角三角形斜边上的中线等于斜边的一半).
=3(直角三角形斜边上的中线等于斜边的一半).
【解析】求GF的长,可以先求GE、FE的长,E为AB边的中点,得出AE的长是解决此问题的途径,通过证明△AEG∽△BFE可以得出.
【考点精析】关于本题考查的正方形的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过 点A,C 画一条射线AE,AE就是∠PRQ的平分线。此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE。则说明这两个三角形全等的依据是( )

A. SSS B. SAS C. ASA D. AAS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力。如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点 C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又 AB=500km,以台风中心为圆心周围250km以内为受影响区域。

(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以平行四边形ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数y= ![]() 的图象交BC于D,连接AD,则四边形AOCD的面积是( )
的图象交BC于D,连接AD,则四边形AOCD的面积是( ) 
A.6
B.7
C.9
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆大坪时代天街已成为人们周末休闲娱乐的重要场所,时代天街从一楼到二楼有一自动扶梯(如图1),图2是侧面示意图.已知自动扶梯AC的坡度为i=1:2.4,AC=13m,BE是二楼楼顶,EF∥MN,B是EF上处在自动扶梯顶端C正上方的一点,且BC⊥EF,在自动扶梯底端A处测得B点仰角为42°.(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90) 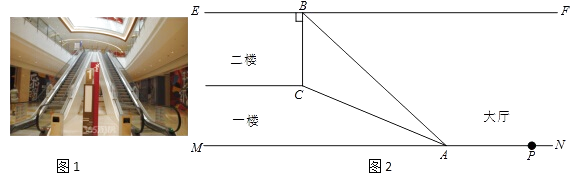
为了吸引顾客,开发商想在P处放置一个高10m的《疯狂动物城》的装饰雕像,并要求雕像最高点与二楼顶层要留出2m距离好放置灯具,请问这个雕像能放得下吗?如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在由6个边长为1的小正方形组成的方格中:
(1)如图(1),A、B、C是三个格点(即小正方形的顶点),判断AB与BC的关系,并说明理由;
(2)如图(2),连结三格和两格的对角线,求∠α+∠β的度数(要求:画出示意图并给出证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生体质情况,从各年级随机抽取部分学生进行体能测试,每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级.统计员在将测试数据绘制成图表时发现,优秀漏统计![]() 人,良好漏统计
人,良好漏统计![]() 人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
(1)填写统计表.
(2)根据调整后数据,补全条形统计图.
(3)若该校共有学生![]() 人,请你估算出该校体能测试等级为“优秀”的人数.
人,请你估算出该校体能测试等级为“优秀”的人数.
学生体能测试成绩各等次人数统计表
体能等级 | 调整前人数 | 调整后人数 |
优秀 |
| |
良好 |
| |
及格 |
| |
不及格 |
| |
合计 |
|
学生体能测试成绩各等次人数统计图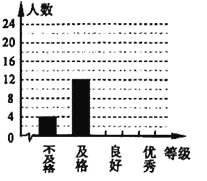
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料并解决有关问题:
我们知道:|x|= .现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
.现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
①x<﹣1;②﹣1≤x<2;③x≥2.
从而化简代数式|x+1|+|x﹣2|可分以下3种情况:
①当x<﹣1时,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1;
②当﹣1≤x<2时,原式=x+1﹣(x﹣2)=3;
③当x≥2时,原式=x+1+x﹣2=2x﹣1.综上讨论,原式= .
.
通过以上阅读,请你解决以下问题:
(1)化简代数式|x+2|+|x﹣4|.
(2)求|x﹣1|﹣4|x+1|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com