
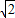 AD.
AD.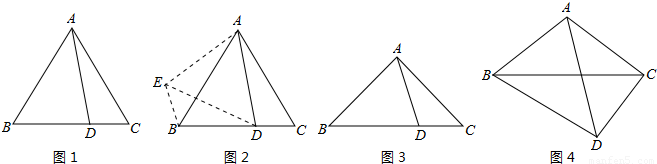
 AD,在△DBE中利用两边之和大于第三边即可得到;
AD,在△DBE中利用两边之和大于第三边即可得到; AD,在△BED中,利用三角形三边关系定理即可证得;
AD,在△BED中,利用三角形三边关系定理即可证得; 解:(1)证明:把△ACD绕点A顺时针旋转90°得到△ABE,连接ED
解:(1)证明:把△ACD绕点A顺时针旋转90°得到△ABE,连接ED AD
AD AD;
AD; 把△ABD旋转,使AB与AC重合,然后绕AC旋转,得到△ACD′,
把△ABD旋转,使AB与AC重合,然后绕AC旋转,得到△ACD′, AD
AD AD.
AD. AD;
AD;

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
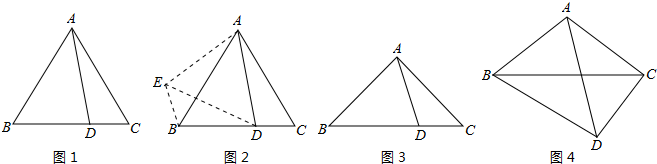
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2014届江苏吴江七年级下期期末调研数学试卷(解析版) 题型:选择题
如图,下列推理及所注明的理由都正确的是
A.∵∠A=∠D(已知)∴AB∥DE(同位角相等,两直线平行)
B.∵∠B=∠DEF(已知) ∴AB∥DE(两直线平行,同位角相等)
C.∵∠A+∠AOE=180°(已知)∴AC∥DF(同旁内角互补,两直线平行)
D.∵AC∥DF(已知) ∴∠F+∠ACF=180°(两直线平行,同旁内角互补)

查看答案和解析>>
科目:初中数学 来源: 题型:
给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)在你学过的特殊四边形中,写出两种勾股四边形的名称:__________和_________;
(2)如图1,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4).请画出以格点
 为顶点,
为顶点,![]() 为勾股边,且对角线相等的勾股四边形
为勾股边,且对角线相等的勾股四边形![]() ;
;
 |
(3)如图2,将![]() 绕顶点
绕顶点![]() 按顺时针方向旋转
按顺时针方向旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,
,
已知![]() .
.
求证:![]() ,即四边形
,即四边形![]() 是勾股四边形.
是勾股四边形.
查看答案和解析>>
科目:初中数学 来源:2012年北京市延庆县中考数学一模试卷(解析版) 题型:解答题
 AD.
AD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com