
分析 (1)画出直线y=-x+2的图象,直接由图象得出“好点”的坐标;
(2)根据反比例函数关于原点对称,直接得出结论;
(3)由题意利用根与系数的关系得出得$\frac{ax}{(x+1)^{2}}+\frac{b}{x+1}+\frac{c}{x}$=$\frac{a}{x+\frac{1}{x}+2}+\frac{b}{x+1}+\frac{c}{x}$求出x1,x2,进而求出k,验证满足△=(2k+1)2-4k(2k-1)=-4k2+8k+1>0,最后分两种情况讨论计算.
解答 解:(1)如图,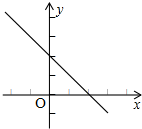
由直线y=-2+2的图象得出它与两坐标轴围成的平面图形中(含边界),
所有“好点”的坐标为(0,0),(1,0),(2,0),(0,1),(0,2),(1,1),
(2)∵k为正整数,k=xy,
∴k至少能够分解成一组两个正整数的乘积,
∴在$y=\frac{k}{x}$位于第一象限的图象上至少有一个“好点”,
∵双曲线的图象关于原点对称,
∴函数y=$\frac{k}{x}$(k为正整数)的图象上必定含有偶数个“好点”,
(3)∵二次函数y=kx2+(2k+1)x+2k-1的图象与x轴相交得到两个不同的“好点”,
∴当k≠0时,关于x的二次方程kx2+(2k+1)x+2k-1=0有两个不等的整数根x1,x2,
∴△=(2k+1)2-4k(2k-1)=-4k2+8k+1>0,①
根据根与系数的关系得,$\frac{ax}{(x+1)^{2}}+\frac{b}{x+1}+\frac{c}{x}$=$\frac{a}{x+\frac{1}{x}+2}+\frac{b}{x+1}+\frac{c}{x}$②
消去k得,(x2-1)(x1-1)=5,
∵x2,x1是整数,
∴$\left\{\begin{array}{l}{{x}_{2}-1=1}\\{{x}_{1}-1=5}\end{array}\right.$或$\left\{\begin{array}{l}{{x}_{2}-1=5}\\{{x}_{1}-1=1}\end{array}\right.$或$\left\{\begin{array}{l}{{x}_{2}-1=-1}\\{{x}_{1}-1=-5}\end{array}\right.$或$\left\{\begin{array}{l}{{x}_{2}-1=-5}\\{{x}_{1}-1=-1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{x}_{2}=2}\\{{x}_{1}=6}\end{array}\right.$或$\left\{\begin{array}{l}{{x}_{2}=6}\\{{x}_{1}=2}\end{array}\right.$或$\left\{\begin{array}{l}{{x}_{2}=0}\\{{x}_{1}=-4}\end{array}\right.$或$\left\{\begin{array}{l}{{x}_{2}=-4}\\{{x}_{1}=0}\end{array}\right.$,∴k=-$\frac{1}{10}$或k=$\frac{1}{2}$,
而k=-$\frac{1}{10}$或k=$\frac{1}{2}$时,均满足△>0,
①当时$k=-\frac{1}{10}$,此时$y=-\frac{1}{10}{x^2}+\frac{4}{5}x-\frac{6}{5}=-\frac{1}{10}(x-2)(x-6)=\frac{2}{5}-\frac{1}{10}{(x-4)^2}$.
由其图象可以得到:其图象与x轴所围成的平面图形中(含边界),一共包含有5个“好点”.
②当时$k=\frac{1}{2}$,此时$y=\frac{1}{2}{x^2}+2x=\frac{1}{2}(x+4)x=\frac{1}{2}{(x+2)^2}-2$.
由其图象可以得到:其图象与x轴所围成的平面图形中(含边界),一共包含有9个“好点”.
点评 此题是二次函数综合题,主要考查了新定义的理解,反比例函数的性质,一元二次方程的根与系数的关系,根的判别式,解本题的根据是理解并灵活运用新定义.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
 定义:对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n,有m≤y≤n,我们就称此函数是在[m,n]范围内的“标准函数.”例如:函数y=-x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,有1≤y≤3,所以说函数y=-x+4是在[1,3]范围内的“标准函数.”
定义:对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n,有m≤y≤n,我们就称此函数是在[m,n]范围内的“标准函数.”例如:函数y=-x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,有1≤y≤3,所以说函数y=-x+4是在[1,3]范围内的“标准函数.”查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=x2-(k+2)x+$\frac{5k+2}{4}$和直线y=(k+1)x+(k+1)2.
已知抛物线y=x2-(k+2)x+$\frac{5k+2}{4}$和直线y=(k+1)x+(k+1)2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 选 手 | 甲 | 乙 | 丙 | 丁 |
| 平均数(环) | 9.2 | 9.2 | 9.2 | 9.2 |
| 方差(环2) | 0.35 | 0.15 | 0.25 | 0.27 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com