
 如图,直线y=$\sqrt{3}$x+$\sqrt{3}$与x轴,y轴分别交于A,B两点,∠OAB的角平分线与OB的垂直平分线相交于P点.
如图,直线y=$\sqrt{3}$x+$\sqrt{3}$与x轴,y轴分别交于A,B两点,∠OAB的角平分线与OB的垂直平分线相交于P点.分析 (1)先求出A、B的坐标,得出OA、OB,由勾股定理求出AB,求出∠OAB=60°,得出∠ABO=30°,再由角平分线的性质得出OG、求出EG,由三角函数求出PE,即可得出点P的坐标;
(2)由线段垂直平分线的性质得出PB=PO,得出∠PBO=∠POE=30°,∠BPE=∠OPE=60°,∠BPM=90°,再由角平分线得出∠MBG=15°,求出∠PBM=45°,即可得出结论.
解答 解:(1)∵直线y=$\sqrt{3}$x+$\sqrt{3}$与x轴,y轴分别交于A,B两点,
当y=0时,x=-1,当x=0时,y=$\sqrt{3}$,
∴A(-1,0),B(0,$\sqrt{3}$),
∴OA=1,OB=$\sqrt{3}$,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2,tan∠OAB=$\frac{OB}{OA}$=$\sqrt{3}$,
∴∠OAB=60°,
∴∠ABO=30°,
∵AP是∠OAB的平分线,
∴∠OAP=30°,$\frac{OG}{BG}=\frac{OA}{AB}$=$\frac{1}{2}$,
∴OG=$\frac{1}{2}$BG=$\frac{OB}{3}$=$\frac{\sqrt{3}}{3}$,
∵PE垂直平分OB,
∴OE=$\frac{1}{2}$OB=$\frac{\sqrt{3}}{2}$,PE∥OA,
∴EG=OE-OG=$\frac{\sqrt{3}}{6}$,∠EPG=∠OAP=30°,
∴PE=$\sqrt{3}$EG=$\sqrt{3}$×$\frac{\sqrt{3}}{6}$=$\frac{1}{2}$,
∴点P的坐标为:($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);
(2)△PBM是等腰直角三角形;理由如下:连接OP,设AP交OB于G,如图所示: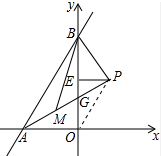 由(1)得:OE=$\frac{\sqrt{3}}{2}$,PE=$\frac{1}{2}$,
由(1)得:OE=$\frac{\sqrt{3}}{2}$,PE=$\frac{1}{2}$,
∴∠POE=30°,
∴∠OPE=60°,
∵PE垂直平分OB,
∴PB=PO,
∴∠PBO=∠POE=30°,∠BPE=∠OPE=60°,
∴∠BPM=∠BPE+∠EPG=90°,
∵BM是∠ABO的平分线,
∴∠MBG=$\frac{1}{2}$∠ABO=15°,
∴∠PBM=30°+∠15°=45°,
∴∠PMB=45°,
∴PB=PM,
即△PBM是等腰直角三角形.
点评 本题是一次函数综合题目,考查了图形与坐标特征、勾股定理、三角函数、角平分线的性质、线段垂直平分线的性质等知识;本题难度较大,综合性强,需要通过作辅助线运用角平分线的性质、线段垂直平分线的性质以及多次运用三角函数才能得出结果.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
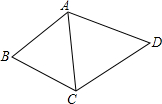 如图,四边形ABCD中,BA=BC,DA=DC,且sin∠D=$\frac{3}{5}$,∠B=45°,则$\frac{{S}_{△ABC}}{{S}_{△ADC}}$=$\frac{\sqrt{2}+1}{3}$.
如图,四边形ABCD中,BA=BC,DA=DC,且sin∠D=$\frac{3}{5}$,∠B=45°,则$\frac{{S}_{△ABC}}{{S}_{△ADC}}$=$\frac{\sqrt{2}+1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
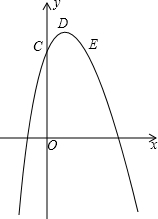 如图,已知抛物线的顶点坐标为D(1,5),抛物线与y轴交于点C(0,4),点C和点E关于对称轴对称.
如图,已知抛物线的顶点坐标为D(1,5),抛物线与y轴交于点C(0,4),点C和点E关于对称轴对称.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com