
【题目】九(3)班“2016年新年联欢会”中,有一个摸奖游戏,规则如下:有4张纸牌,背面都是喜羊羊头像,正面有2张笑脸、2张哭脸.现将4张纸牌洗匀后背面朝上摆放到桌上,然后让同学去翻纸牌.
(1)现小芳有一次翻牌机会,若正面是笑脸的就获奖,正面是哭脸的不获奖.她从中随机翻开一张纸牌,则小芳获奖的概率是 ;
(2)如果小芳、小明都有翻两张牌的机会.小芳先翻一张,放回洗匀后再翻一张;小明同时翻开两张纸牌.他们各自翻开的两张纸牌中只要出现笑脸就获奖.他们获奖的机会相等吗?分析说明理由.
【答案】(1)![]() ;(2)机会不相等.理由参见解析.
;(2)机会不相等.理由参见解析.
【解析】
试题分析:(1)根据正面有2张笑脸、2张哭脸,直接利用概率公式求解即可求得答案;(2)首先根据题意分别列出表格,然后由表格即可求得所有等可能的结果与获奖的情况,再利用概率公式求解即可求得他们获奖的概率,比较即可求得答案.
试题解析:(1)∵有4张纸牌,背面都是喜羊羊头像,正面有2张笑脸、2张哭脸,翻一次牌正面是笑脸的就获奖,正面是哭脸的不获奖,∴获奖的概率是![]() ;故答案为:
;故答案为:![]() ;(2)他们获奖机会不相等,理由如下:
;(2)他们获奖机会不相等,理由如下:
小芳:
第一张 第二张 | 笑1 | 笑2 | 哭1 | 哭2 |
笑1 | 笑1,笑1 | 笑2,笑1 | 哭1,笑1 | 哭2,笑1 |
笑2 | 笑1,笑2 | 笑2,笑2 | 哭1,笑2 | 哭2,笑2 |
哭1 | 笑1,哭1 | 笑2,哭1 | 哭1,哭1 | 哭2,哭1 |
哭2 | 笑1,哭2 | 笑2,哭2 | 哭1,哭2 | 哭2,哭2 |
∵共有16种等可能的结果,翻开的两张纸牌中只要出现笑脸的有12种情况,∴P(小芳获奖)=![]() =
=![]() ;
;
小明:
第一张 第二张 | 笑1 | 笑2 | 哭1 | 哭2 |
笑1 | 笑2,笑1 | 哭1,笑1 | 哭2,笑1 | |
笑2 | 笑1,笑2 | 哭1,笑2 | 哭2,笑2 | |
哭1 | 笑1,哭1 | 笑2,哭1 | 哭2,哭1 | |
哭2 | 笑1,哭2 | 笑2,哭2 | 哭1,哭2 |
∵共有12种等可能的结果,翻开的两张纸牌中只要出现笑脸的有10种情况,∴P(小明获奖)=![]() =
=![]() ,∵P(小芳获奖)≠P(小明获奖),∴他们获奖的机会不相等.
,∵P(小芳获奖)≠P(小明获奖),∴他们获奖的机会不相等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下列函数解析式:h=﹣3(t﹣2)2+5,则小球距离地面的最大高度是( )
A.2米
B.3米
C.5米
D.6米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,圆柱的高是4厘米,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化. 
(1)在这个变化过程中,自变量是 , 因变量是 .
(2)圆柱的体积V与底面半径r的关系式是 .
(3)当圆柱的底面半径由2变化到8时,圆柱的体积由cm3变化到cm3 .
查看答案和解析>>
科目:初中数学 来源: 题型:
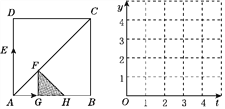
【题目】如图,正方形ABCD的边长为4,动点E从点A出发,以每秒2个单位的速度沿A→D→A运动,动点G从点A出发,以每秒1个单位的速度沿A→B运动,当有一个点到达终点时,另一点随之也停止运动.过点G作FG⊥AB交AC于点F.设运动时间为t(单位:秒).以FG为一直角边向右作等腰直角三角形FGH,△FGH与正方形ABCD重叠部分的面积为S.
(1)当t=1.5时,S=________;当t=3时,S=________.
(2)设DE=y1,AG=y2,在如图所示的网格坐标系中,画出y1与y2关于t的函数图象.并求当t为何值时,四边形DEGF是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一周内,小明坚持自测体温,每天3次.测量结果统计如下表:
体温(℃) | 36.1 | 36.2 | 36.3 | 36.4 | 36.5 | 36.6 | 36.7 |
次数 | 2 | 3 | 4 | 6 | 3 | 1 | 2 |
则这些体温的中位数是( )
A. 36.2℃B. 36.3℃C. 36.4℃D. 36.5℃
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED. 
(1)探究猜想: ①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③猜想图1中∠AED,∠EAB,∠EDC的关系并证明你的结论.
(2)拓展应用: 如图2,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③、④位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(不要求证明).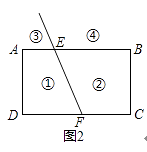
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com