
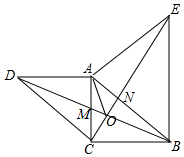
 已知:如图,△ABC中,∠ACB=90°,AC=BC,以A为直角顶点,分别以AC、AB为一直角边,在△ABC外做等腰直角△ACD和△ABE,连接BD、CE交与点O.
已知:如图,△ABC中,∠ACB=90°,AC=BC,以A为直角顶点,分别以AC、AB为一直角边,在△ABC外做等腰直角△ACD和△ABE,连接BD、CE交与点O.分析 (1)证明△DAB≌△CAE(SAS),可以得出BD=CE,∠ADB=∠ACE,再利用△AMD和△OMC中,两个角相等,则根据三角形的内角和定理可知:∠COM=∠MAD=90°,则BD⊥CE;
(2)作高线AG、AH,由全等可知面积相等,底边相等,则高AG=AH;根据角平分线的逆定理得:AO平分∠MON;
(3)先证明四边形ADCB是平行四边形,则AM=MC,DM=BM,设AM=x,则CM=x,AD=2x,DM=$\sqrt{5}$x,
分别表示出AM和AN的长,相比即可.
解答  解:(1)BD=CE,且BD∥CE,理由是:
解:(1)BD=CE,且BD∥CE,理由是:
∵△ACD和△ABE是等腰直角三角形,
∴AC=AD,AB=AE,∠DAC=∠BAE=90°,
∴∠DAC+∠CAB=∠BAE+∠CAB,
即∠DAB=∠CAE,
∴△DAB≌△CAE(SAS),
∴BD=CE,∠ADB=∠ACE,
∵∠AMD=∠OMC,
∴∠COM=∠MAD=90°,
∴BD⊥CE;
(2)过A作AG⊥BD于G,作AH⊥EC于H,
∵△DAB≌△CAE,
∴S△DAB=S△CAE,
∴$\frac{1}{2}$BD•AG=$\frac{1}{2}$CE•AH,
∵BD=CE,
∴AG=AH,
∴AO平分∠MON;
(3)∵AD=AC,
∵∠DAC=∠ACB=90°,
∴AD∥BC,
∴四边形ADCB是平行四边形,
∴AM=MC,DM=BM,
设AM=x,则CM=x,AD=2x,DM=$\sqrt{5}$x,
∵tan∠MDA=tan∠MCO=$\frac{AM}{AD}$=$\frac{OM}{OC}$=$\frac{1}{2}$,
∴OM=$\frac{\sqrt{5}}{5}$x,OC=$\frac{2\sqrt{5}}{5}$x,
∴OB=$\frac{4\sqrt{5}}{5}$x,
∵DC∥BN,
∴△DCO∽△BNO,
∴$\frac{DC}{BN}=\frac{DO}{OB}$,
∴$\frac{2\sqrt{2}x}{BN}=\frac{\frac{6\sqrt{5}}{5}x}{\frac{4\sqrt{5}}{5}x}$,
∴BN=$\frac{4\sqrt{2}}{3}$x,
∴AN=AB-BN=2$\sqrt{2}$x-$\frac{4\sqrt{2}}{3}$x=$\frac{2\sqrt{2}}{3}$x,
∴$\frac{AM}{AN}$=$\frac{x}{\frac{2\sqrt{2}}{3}x}$=$\frac{3\sqrt{2}}{4}$.
点评 本题是三角形的综合题,考查了等腰直角三角形的性质、角平分线性质定理的逆定理、三角形相似和全等的性质和判定、同角的三角函数等知识,运用的知识点较多,第二问巧用面积法,证明高线相等,根据角平分线性质定理的逆定理得出结论,第三问关键是根据同角的三角函数确定OC=2OM,并设未知数求解.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.5米 | B. | 1米 | C. | 1.5米 | D. | 2米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com