
分析 (1)将已知比例式化为乘积式得:m+3=k(c-n),m(m-1)=k(n+c),两式相加后化成比例式可得结论;
(2)先根据条件得:k>0,由式子$\frac{m+3}{c-n}$>0和m+3>0得:c-n>0,则c>n;
(3)将k=2代入已知比例式中,化为乘积式后列方程组,可得:c>m,则c是△MNC的最大边,即MN是的△MNC最大边.
解答 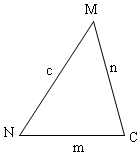 证明:(1)∵k=$\frac{m+3}{c-n}$=$\frac{m(m-1)}{n+c}$,
证明:(1)∵k=$\frac{m+3}{c-n}$=$\frac{m(m-1)}{n+c}$,
∴m+3=k(c-n),m(m-1)=k(n+c),
∴m+3+m(m-1)=k(c-n)+k(n+c),
∴m2+3=2kc,
∴k=$\frac{{m}^{2}+3}{2c}$;
(2)∵k=$\frac{{m}^{2}+3}{2c}$,c>0,m2+3>0,
∴k>0,
∴$\frac{m+3}{c-n}$>0,
∵m+3>0,
∴c-n>0,
∴c>n;
(3)∵k=2,
∴$\frac{m+3}{c-n}$=$\frac{m(m-1)}{n+c}$=2,
∴$\left\{\begin{array}{l}{m+3=2c-2n①}\\{{m}^{2}-m=2n+2c②}\end{array}\right.$,
②-①得:m2-2m-3=4n>0,
∴(m-3)(m+1)>0,
∵m+1>0,
∴m-3>0,
∴m>3,
①+②得:m2+3=4c,
∴m2-4m+3=4c-4m,
(m-3)(m-1)=4c-4m,
∵$\frac{m(m-1)}{n+c}$=2,m>0,n+c>0,
∴m-1>0,
∴m>1,
∴4c-4m>0,
∴c>m,
由(2)得:c>n,
∴c是△MNC的最大边,
即:MN是的△MNC最大边.
点评 本题是三角形的综合题,考查了比例的性质、不等式和等式的性质、因式分解,第3问有难度,应用二次三项式的因式分解与同号得正数的原理解决问题,本题熟练掌握比例的性质是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 361×106 | B. | 36.1×107 | C. | 3.61×108 | D. | 3.61×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
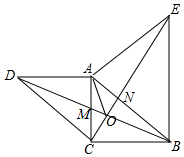 已知:如图,△ABC中,∠ACB=90°,AC=BC,以A为直角顶点,分别以AC、AB为一直角边,在△ABC外做等腰直角△ACD和△ABE,连接BD、CE交与点O.
已知:如图,△ABC中,∠ACB=90°,AC=BC,以A为直角顶点,分别以AC、AB为一直角边,在△ABC外做等腰直角△ACD和△ABE,连接BD、CE交与点O.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
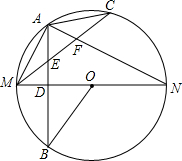 如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为弧AN上一点,且$\widehat{AC}$=$\widehat{AM}$,连接CM,交AB于点E,交AN于点F,现给出以下结论:①MD=DO;②$\widehat{AM}$=$\widehat{BM}$;③∠ACM+∠ANM=∠MOB;④AE=$\frac{1}{2}$MF.其中正确的结论有②③④.(请把所有正确结论的序号都填在横线上)
如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为弧AN上一点,且$\widehat{AC}$=$\widehat{AM}$,连接CM,交AB于点E,交AN于点F,现给出以下结论:①MD=DO;②$\widehat{AM}$=$\widehat{BM}$;③∠ACM+∠ANM=∠MOB;④AE=$\frac{1}{2}$MF.其中正确的结论有②③④.(请把所有正确结论的序号都填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com