
分析 (1)、(2)分别把各方程组中的方程化为不含分母及括号的方程,再用代入消元法和加减消元法求解即可.
解答 解:(1)原方程组可化为$\left\{\begin{array}{l}{2x+5y=8①}\\{2x+3y=12②}\end{array}\right.$,
①-②得,2y=-4,解得y=-2,把y=-2代入①得,2x-10=8,解得x=9,
故原方程组的解为$\left\{\begin{array}{l}{x=9}\\{y=-2}\end{array}\right.$;
(2)原方程组可化为$\left\{\begin{array}{l}{2x-3y=8①}\\{x+3y=1②}\end{array}\right.$,
①+②得,3x=9,解得x=3,把x=3代入②得,3+3y=1,解得y=-$\frac{2}{3}$.
故原方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-\frac{2}{3}}\end{array}\right.$.
点评 本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$<k≤3 | B. | 2<k≤3 | C. | 2≤k≤3 | D. | $\frac{3}{2}$<k≤2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
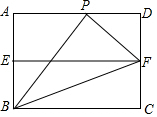 如图,在矩形ABCD中,AB=2,AD=3,E、F分别是AB、CD的中点,P是AD上一点,∠PFB=3∠FBC,则线段PD的长度$\frac{4}{3}$.
如图,在矩形ABCD中,AB=2,AD=3,E、F分别是AB、CD的中点,P是AD上一点,∠PFB=3∠FBC,则线段PD的长度$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,?ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,若EF的长为6$\sqrt{3}$,求AB的长.
如图,?ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,若EF的长为6$\sqrt{3}$,求AB的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com