
分析 (1)根据题意可以求得w关于n的函数关系式,由购买A笔记本的数量要少于B笔记本数量的$\frac{2}{3}$,但又不少于B笔记本数量的$\frac{1}{3}$,可以确定n的取值范围;
(2)根据(1)中的函数关系式可以求得w的最小值及此时购买的A和B种两种笔记本的数量.
解答 解:(1)依题意得:w=12n+8(30-n)
即w=4n+240
且n<$\frac{2}{3}$(30-n)和n≥$\frac{1}{3}$(30-n)
解得$\frac{15}{2}$≤n<12
所以,w(元)关于n(本)的函数关系式为:w=4n+240
自变量n的取值范围是$\frac{15}{2}$≤n<12,n为整数;
(2)对于一次函数w=4n+240
∵w随n的增大而增大,且$\frac{15}{2}$≤n<12,n为整数
故当n为8时,w的值最小
此时,30-n=30-8=22,w=4×8+240=272(元)
因此,当买A种笔记本8本、B种笔记本22本时,所花费用最少,为272元.
点评 本题考查了一次函数的应用,一元一次不等式的应用.此题利用了(总花费=A种笔记本的单位价×A的数量+B种笔记本的单位价×B的数量),还用到了解不等式组以及一次函数的有关性质(当k>0时,y随x的增大而增大).


科目:初中数学 来源: 题型:解答题
 如图,AB是半圆O的直径,D是弧BC的中点,四边形ABCD的对角线AD、BC交于点E,AC、BD的延长线交于点F
如图,AB是半圆O的直径,D是弧BC的中点,四边形ABCD的对角线AD、BC交于点E,AC、BD的延长线交于点F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
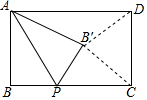 如图,在矩形ABCD中,AB=a,BC=b,点P是BC上的一个动点,连接AP,把△PAB沿着AP翻折到△PB′C(点B′在矩形的内部),连接B′C,B′D.点P在整个运动过程中,若存在唯一的位置使得△B′CD为直角三角形,则a,b之间的数量关系是b=$\sqrt{2}$a.
如图,在矩形ABCD中,AB=a,BC=b,点P是BC上的一个动点,连接AP,把△PAB沿着AP翻折到△PB′C(点B′在矩形的内部),连接B′C,B′D.点P在整个运动过程中,若存在唯一的位置使得△B′CD为直角三角形,则a,b之间的数量关系是b=$\sqrt{2}$a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com