
分析 本题涉及零指数幂、负指数幂、二次根式化简3个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答 解:(1)2-1+$\sqrt{4}$-$\root{3}{8}$+($\sqrt{2}$)0
=$\frac{1}{2}$+2-2+1
=$\frac{3}{2}$;
(2)$\sqrt{16}$+$\root{3}{(-2)^{3}}$-|2-$\sqrt{3}$|
=4-2-2+$\sqrt{3}$
=$\sqrt{3}$.
点评 本题主要考查了实数的综合运算能力,是中考常见题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等相关知识.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
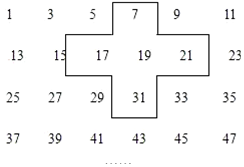 实践与探索:将连续的奇数1,3,5,7…排列成如图的数表用十字框框出5个数(如图)
实践与探索:将连续的奇数1,3,5,7…排列成如图的数表用十字框框出5个数(如图)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-$\frac{1}{3}$(x-5)2 | B. | y=-$\frac{1}{3}$x2-5 | C. | y=-$\frac{1}{3}$(x+5)2 | D. | y=$\frac{1}{3}$(x+5)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{{3}^{5}}{5×{2}^{9}}$ | B. | $\frac{5×{3}^{5}}{{2}^{12}}$ | C. | $\frac{5×{3}^{6}}{{2}^{14}}$ | D. | $\frac{{3}^{7}}{5×{2}^{11}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com