
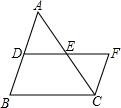
 如图,在△ABC中,D、E分别为AB、AC的中点,延长DE到F,使EF=DE,若AB=10,
如图,在△ABC中,D、E分别为AB、AC的中点,延长DE到F,使EF=DE,若AB=10, 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源: 题型:
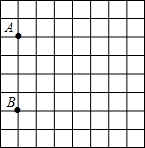 有一张图纸被损坏,但上面有如图的两个标志点A(-3,1),B(-3,3)可认,而主要建筑C(3,2)破损,请通过建立直角坐标系找到图中C点的位置,并求△ABC的周长.
有一张图纸被损坏,但上面有如图的两个标志点A(-3,1),B(-3,3)可认,而主要建筑C(3,2)破损,请通过建立直角坐标系找到图中C点的位置,并求△ABC的周长.查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 8 |
| 2 |
| 1 |
| 2 |
| 2 |
| 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
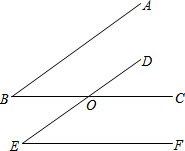 已知如图BC交DE于O,给出下面三个论断:
已知如图BC交DE于O,给出下面三个论断:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在10×6的正方形网格中,每个小正方形的边长均为单位1,将△ABC向右平移5个单位,得到△A′B′C′,再把△A′B′C′绕点A′顺时针旋转90°,得到△A″B″C″,请你画出△A′B′C′和△A″B″C″(不要求写画法).
如图,在10×6的正方形网格中,每个小正方形的边长均为单位1,将△ABC向右平移5个单位,得到△A′B′C′,再把△A′B′C′绕点A′顺时针旋转90°,得到△A″B″C″,请你画出△A′B′C′和△A″B″C″(不要求写画法).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com