
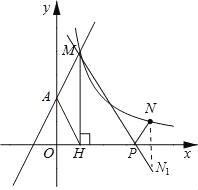
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数y=![]() (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)4;(2)存在,P点坐标为(![]() ,0).
,0).
【解析】
试题分析:(1)根据直线解析式求A点坐标,得OA的长度;根据三角函数定义可求OH的长度,得点M的横坐标;根据点M在直线上可求点M的坐标.从而可求K的值;(2)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置.
试题解析:(1)由y=2x+2可知A(0,2),即OA=2.∵tan∠AHO=2,∴OH=1.∵MH⊥x轴,∴点M的横坐标为1.∵点M在直线y=2x+2上,∴点M的纵坐标为4.即M(1,4).∵点M在y=![]() 上,∴k=1×4=4.(2)存在.过点N作N关于x轴的对称点N1,连接MN1,交x轴于P(如图所示).此时PM+PN最小.∵点N(a,1)在反比例函数y=
上,∴k=1×4=4.(2)存在.过点N作N关于x轴的对称点N1,连接MN1,交x轴于P(如图所示).此时PM+PN最小.∵点N(a,1)在反比例函数y=![]() (x>0)上,∴a=4.即点N的坐标为(4,1).∵N与N1关于x轴的对称,N点坐标为(4,1),∴N1的坐标为(4,﹣1).设直线MN1的解析式为y=kx+b.由
(x>0)上,∴a=4.即点N的坐标为(4,1).∵N与N1关于x轴的对称,N点坐标为(4,1),∴N1的坐标为(4,﹣1).设直线MN1的解析式为y=kx+b.由![]() 解得k=﹣
解得k=﹣![]() ,b=
,b=![]() .∴直线MN1的解析式为y=﹣
.∴直线MN1的解析式为y=﹣![]() x+
x+![]() .令y=0,得x=
.令y=0,得x=![]() .∴P点坐标为(
.∴P点坐标为(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将点P(-2,3)沿x轴方向向右平移3个单位得到点Q,则点Q的坐标是( )
A.(-2,6)
B.(-2,0)
C.(-5,3)
D.(1,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年暑假,张华组织本班同学一起去看著名影星吴京自导自演的电影《战狼2》,票价每张60元,20张以上(不含20张)可以打八折,他们一共花了1200元,他们共买了张电影票.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线经过A![]() ,B
,B![]() ,C
,C![]() 三点.
三点.
(1)求抛物线的解析式。
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8cm,BC=16cm,点P从点A沿边AB向点B以1cm/s的速度移动,同时点Q从点B沿边BC向点C以2cm/s的速度移动,有一点到终点运动即停止,设运动时间为t秒.
(1)t为何值时,△PBQ的面积为12cm2;
(2)若PQ⊥DQ,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a=﹣34 , b=(﹣3)4 , c=(23)4 , d=(22)6 , 则下列四数关系的判断,何者正确?( )
A.a=b,c=d
B.a=b,c≠d
C.a≠b,c=d
D.a≠b,c≠d
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com