解:(1)∵MN∥BC,∴△AMN∽△ABC
∴S
△AMN:S
△ABC=(
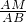
)
2,
即S
△AMN:5=x
2,
∵S
△MBN:S
△AMN=

-1,
∴S
△MBN=-5x
2+5x
∴y=-5x
2+5x(0<x<1);
(2)∵E、F分别是边AB,AC的中点,∴FE∥BC∥MN,
①当0<x≤

时,△MBN与△EBF的公共部分的三角形与△MBN相似,
∴y:S=4(1-x)
2,∴S=
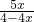
,
②当

<x<1时,△MBN与△EBF的公共部分的三角形与△EBF相似,
∴S:S
△BEF=4(1-x)
2,
∵S
△BEF=

,
∴S=5(1-x)
2;
(3)当S=

时,x=
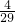
或x=

.
分析:(1)由MN∥BC可知△AMN∽△ABC,得到S
△AMN:S
△ABC=(
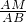
)
2,即S
△AMN:5=x
2,利用相似的面积比等于相似比的平方可求得S
△MBN=-5x
2+5x,即y=-5x
2+5x(0<x<1);
(2)根据FE∥BC∥MN可知,
①当0<x≤

时,△MBN与△EBF的公共部分的三角形与△MBN相似,利用相似的面积比等于相似比的平方可求得S=
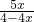
;
②当

<x<1时,△MBN与△EBF的公共部分的三角形与△EBF相似,利用相似的面积比等于相似比的平方可求得S=5(1-x)
2;
(3)当S=

时,x=
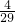
或x=

.
点评:主要考查了相似三角形的性质和根据实际问题列二次函数关系式,其中涉及到直接开平方法解一元二次方程的方法;要会根据几何图形之间的关系列一元二次方程,利用相似三角形的相似比是解题的关键.

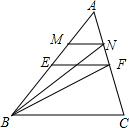 ,连接BN.设
,连接BN.设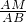 =x,S△MBN=y.
=x,S△MBN=y. 时,试确定x的值.(不必写出解题过程)
时,试确定x的值.(不必写出解题过程)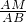 )2,
)2, -1,
-1, 时,△MBN与△EBF的公共部分的三角形与△MBN相似,
时,△MBN与△EBF的公共部分的三角形与△MBN相似,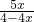 ,
, <x<1时,△MBN与△EBF的公共部分的三角形与△EBF相似,
<x<1时,△MBN与△EBF的公共部分的三角形与△EBF相似, ,
, 时,x=
时,x=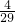 或x=
或x= .
.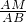 )2,即S△AMN:5=x2,利用相似的面积比等于相似比的平方可求得S△MBN=-5x2+5x,即y=-5x2+5x(0<x<1);
)2,即S△AMN:5=x2,利用相似的面积比等于相似比的平方可求得S△MBN=-5x2+5x,即y=-5x2+5x(0<x<1); 时,△MBN与△EBF的公共部分的三角形与△MBN相似,利用相似的面积比等于相似比的平方可求得S=
时,△MBN与△EBF的公共部分的三角形与△MBN相似,利用相似的面积比等于相似比的平方可求得S=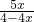 ;
; <x<1时,△MBN与△EBF的公共部分的三角形与△EBF相似,利用相似的面积比等于相似比的平方可求得S=5(1-x)2;
<x<1时,△MBN与△EBF的公共部分的三角形与△EBF相似,利用相似的面积比等于相似比的平方可求得S=5(1-x)2; 时,x=
时,x=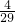 或x=
或x= .
.


 如图,已知△ABC的面积为4,且AB=AC,现将△ABC沿CA方向平移CA的长度,得到△EFA.
如图,已知△ABC的面积为4,且AB=AC,现将△ABC沿CA方向平移CA的长度,得到△EFA.
 (2010•孝感模拟)如图,已知△ABC的三个顶点的坐标分别为A(-2,2)、B(-5,0)、C(-1,0).
(2010•孝感模拟)如图,已知△ABC的三个顶点的坐标分别为A(-2,2)、B(-5,0)、C(-1,0). 如图,已知△ABC的三个顶点的坐标分别是A(-7,1),B(-3,3),C(-2,6).
如图,已知△ABC的三个顶点的坐标分别是A(-7,1),B(-3,3),C(-2,6).