
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知平面直角坐标系中A(-1,3),B(2,0),C(-3,-1).
如图,已知平面直角坐标系中A(-1,3),B(2,0),C(-3,-1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
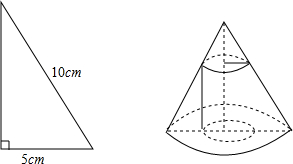
 如图,已知AD是△ABC的中线,AB=6,AC=4,△ACD的面积为6,那么△ABC的面积为12,△ABD与△ACD的周长之差是2,BC边的长可以为5(写出一个即可)
如图,已知AD是△ABC的中线,AB=6,AC=4,△ACD的面积为6,那么△ABC的面积为12,△ABD与△ACD的周长之差是2,BC边的长可以为5(写出一个即可)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
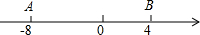 数轴上两个点A,B所对应的数为-8,4,A、B两点各自以一定的速度同时运动,且A点的运动速度为2个单位/秒.
数轴上两个点A,B所对应的数为-8,4,A、B两点各自以一定的速度同时运动,且A点的运动速度为2个单位/秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
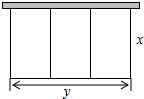 如图所示,猪舍三间,它们的形状是一排大小相等的三个矩形,一面利用旧墙(旧墙长12m),包括隔墙在内的其它各墙均用木料,已知现有木料可围24m的墙,设整个猪舍的长为ym,宽为xm,则y与x的函数关系式为y=24-4x,自变量x的取值范围是3≤x<6.
如图所示,猪舍三间,它们的形状是一排大小相等的三个矩形,一面利用旧墙(旧墙长12m),包括隔墙在内的其它各墙均用木料,已知现有木料可围24m的墙,设整个猪舍的长为ym,宽为xm,则y与x的函数关系式为y=24-4x,自变量x的取值范围是3≤x<6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com