
【题目】如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
(1)当t为何值时,点Q与点D重合?
(2)当⊙Q经过点A时,求⊙P被OB截得的弦长.
(3)若⊙P与线段QC只有一个公共点,求t的取值范围.
【答案】
(1)
解:∵OA=6,OB=8,
∴由勾股定理可求得:AB=10,
由题意知:OQ=AP=t,
∴AC=2t,
∵AC是⊙P的直径,
∴∠CDA=90°,
∴CD∥OB,
∴△ACD∽△ABO,
∴ ![]() ,
,
∴AD= ![]() ,
,
当Q与D重合时,
AD+OQ=OA,
∴ ![]() +t=6,
+t=6,
∴t= ![]() ;
;
(2)
解:当⊙Q经过A点时,如图1,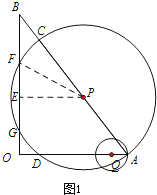
OQ=OA﹣QA=4,
∴t= ![]() =4s,
=4s,
∴PA=4,
∴BP=AB﹣PA=6,
过点P作PE⊥OB于点E,⊙P与OB相交于点F、G,
连接PF,
∴PE∥OA,
∴△PEB∽△AOB,
∴ ![]() ,
,
∴PE= ![]() ,
,
∴由勾股定理可求得:EF= ![]() ,
,
由垂径定理可求知:FG=2EF= ![]() .
.
(3)
解:当QC与⊙P相切时,如图2,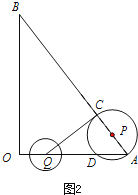
此时∠QCA=90°,
∵OQ=AP=t,
∴AQ=6﹣t,AC=2t,
∵∠A=∠A,
∠QCA=∠ABO,
∴△AQC∽△ABO,
∴ ![]() ,
,
∴ ![]() ,
,
∴t= ![]() ,
,
∴当0<t≤ ![]() 时,⊙P与QC只有一个交点,
时,⊙P与QC只有一个交点,
当QC⊥OA时,
此时Q与D重合,
由(1)可知:t= ![]() ,
,
∴当 ![]() <t≤5时,⊙P与QC只有一个交点,
<t≤5时,⊙P与QC只有一个交点,
综上所述,当,⊙P与QC只有一个交点,t的取值范围为:0<t≤ ![]() 或
或 ![]() <t≤5.
<t≤5.
【解析】(1)由题意知CD⊥OA,所以△ACD∽△ABO,利用对应边的比求出AD的长度,若Q与D重合时,则,AD+OQ=OA,列出方程即可求出t的值; (2)由于0<t≤5,当Q经过A点时,OQ=4,此时用时为4s,过点P作PE⊥OB于点E,利用垂径定理即可求出⊙P被OB截得的弦长;
(3)若⊙P与线段QC只有一个公共点,分以下两种情况,①当QC与⊙P相切时,计算出此时的时间;②当Q与D重合时,计算出此时的时间;由以上两种情况即可得出t的取值范围.本题考查圆的综合问题,涉及圆的切线判定,圆周角定理,相似三角形的判定与性质,学生需要根据题意画出相应的图形来分析,并且能综合运用所学知识进行解答.


科目:初中数学 来源: 题型:
【题目】如图,四边形 ABCD 中,AC=a,BD=b,且 AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,…,如此进行下去,得到四边形AnBnCnDn.下列结论正确的有( )
①四边形A2B2C2D2是矩形;
②四边形A4B4C4D4是菱形;
③四边形A5B5C5D5的周长是![]()
④四边形AnBnCnDn的面积是![]()

A. ①②③ B. ②③④ C. ①② D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( ) 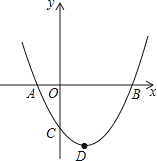
A.2a﹣b=0
B.a+b+c>0
C.3a﹣c=0
D.当a= ![]() 时,△ABD是等腰直角三角形
时,△ABD是等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,我们很熟悉这样的算式:![]() ,其实,数学不仅非常美妙,而且魅力无穷.请你欣赏下列一组等式:
,其实,数学不仅非常美妙,而且魅力无穷.请你欣赏下列一组等式:
①![]()
②![]()
③![]()
④![]()
⑤……
(1)写出第⑤个等式:![]()
(2)根据上述规律,写出第![]() 个等式:
个等式:
![]()
(3)观察比较,并大胆猜想:
![]()
(4)根据(2)的规律计算![]() (写出计算过程)
(写出计算过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.
(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BGBA=48,FG= ![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次男子马拉松长跑比赛中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据:140 146 143 175 125 164 134 155 152 168 162 148
(1)计算该样本数据的中位数和平均数;
(2)如果一名选手的成绩是147分钟,请你依据样本数据中位数,推断他的成绩如何?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com