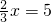练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知-数学公式，可求得x=________，这是根据________．

    ??    等式的性质2
    分析：根据等式的基本性质2可知：由-，可求得x=-．
    解答：根据等式的基本性质2，-两边都乘以-，可求得x=-．
    点评：主要考查了等式的基本性质．
    等式性质：1、等式的两边同时加上或减去同一个数或字母，等式仍成立；
    2、等式的两边同时乘以或除以同一个不为0数或字母，等式仍成立．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    课本中有这么一个例题：“如图，河对岸有一水塔AB．在C处测得塔顶A的仰角为30°，向塔前进12米到达D，在D处测得A的仰角为45°，求水塔AB的高”．
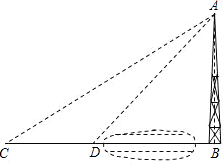    解这个题时，我们通常时这样去想的（分析）：要求水塔AB的高，只要去寻找AB于已知量之间的关系．在这里，由于难以找到四个量之间的直接关系，我们可精英家教网引进一个或两个中间量．以此作为媒介，再寻找这些量之间的关系，得到．于是，就可求得水塔的高，问题就解决了．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：如图①，正方形ABCD与矩形DEFG的边AD、DE在同一直线l上，点G在CD上．正方形ABCD的边长为a，矩形DEFG的长DE为b，宽DG为3（其中a＞b＞3）．若矩形DEFG沿直线l向左以每秒1个单位的长度的速度运动（点D、E始终在直线l上）．若矩形DEFG在运动过程中与正方形ABCD的重叠部分的面积记作S，运动时间记为t秒（0≤t≤m），其中S与t的函数图象如图②所示．矩形DEFG的顶点经运动后的对应点分别记作D′、E′、F′、G′．
    （1）根据题目所提供的信息，可求得b=
     
    ，a=
     
    ，m=
     
    ；
    （2）连接AG′、CF′，设以AG′和CF′为边的两个正方形的面积之和为y，求当0≤t≤5时，y与时间t之间的函数关系式，并求出y的最小值以及y取最小值时t的值；
    （3）如图③，这是在矩形DEFG运动过程中，直线AG′第一次与直线CF′垂直的情形，求此时t的值．并探究：在矩形DEFG继续运动的过程中，直线AG′与直线CF′是否存在平行或再次垂直的情形？如果存在，请画出图形，并求出t的值；否则，请说明理由．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某工厂生产A、B两种型号的帐篷，已知A型帐篷40顶和B型帐篷20顶共重2180kg，A型帐篷10顶和B型帐篷60顶共重2580kg，且每种型号的帐篷都是由防雨布和钢材两种材料制成的．
    （1）求A、B两种型号的帐篷每顶各重多少kg，并根据求得的结果把下表中的空格填上．
    防雨布 钢材
    每顶A型帐篷所需材料 20kg
    每顶B型帐篷所需材料 12kg
    （2）汶川发生特大地震灾害后，该工厂立即用现有的45吨防雨布和28.5吨钢材突击赶制上述两种规格的帐篷2000顶，送往灾区供灾民居住．若设生产A型帐篷x顶
    ①求x的取值范围，并说明共有多少种生产方案．
    ②若每顶A型帐篷可解决10个灾民的居住问题，每顶B型帐篷可解决12个灾民的居住问题，问如何安排生产可最大限度地解决灾民居住问题，最多可解决多少个灾民的居住问题．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•青田县模拟）为了探索代数式
    		x2+1
    +
    		(8-x)2+25
    的最小值，小明巧妙的运用了“数形结合”思想．具体方法是这样的：如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC．已知AB=1，DE=5，BD=8，设BC=x．则AC=
    		x2+1
    ，CE=
    		(8-x)2+25
    ，则问题即转化成求AC+CE的最小值．
    （1）我们知道当A、C、E在同一直线上时，AC+CE的值最小，于是可求得
    		x2+1
    +
    		(8-x)2+25
    的最小值等于
    10
    10
    ，此时x=
    4
    3
    4
    3
    ；
    （2）请你根据上述的方法和结论，试构图求出代数式
    		x2+4
    +
    		(12-x)2+9
    的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：二次函数y=ax2+bx+c（a≠0）中的x和y满足下表：
    x … 0 1 2 3 4 5 …
    y … 3 0 -1 0 m 8 …
    （1）可求得m的值为
    3
    3
    ；
    （2）求出这个二次函数的解析式；
    （3）当0＜x＜3时，则y的取值范围为
    -1≤y＜3
    -1≤y＜3
    ．

    查看答案和解析>>

    同步练习册答案