【题目】如图，在RtΔABC中，∠C=90°，∠BAC的角平分线AD交BC边于D，以AB上某一点O为圆心作⊙O，使⊙O经过点A和点D，与AB边的另一个交点为E.

(1)判断直线BC与⊙O的位置关系，并说明理由;

(2)若⊙O的半径为4，∠B=30°.求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.

参考答案：

【答案】（1）相切，理由见解析；（2）（2）.

【解析】试题分析：（1）连接OD，根据平行线判定推出OD∥AC，推出OD⊥BC，根据切线的判定推出即可；

（2）根据S阴影=S△BOD-S扇形DOE求得即可．

试题解析：（1）直线BC与⊙O相切；
连结OD，

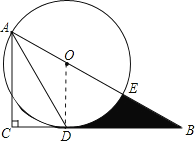
∵OA=OD，
∴∠OAD=∠ODA，
∵∠BAC的角平分线AD交BC边于D，
∴∠CAD=∠OAD，
∴∠CAD=∠ODA，
∴OD∥AC，
∴∠ODB=∠C=90°，
即OD⊥BC．
又∵直线BC过半径OD的外端，
∴直线BC与⊙O相切．

（2）在Rt△ACB中，∠B=30°，
∴∠BOD=60°．
∴．
∵∠B=30°，OD⊥BC，
∴OB=2OD，
∵OD=4

∴OB=8，
∴BD=4

S△BOD=×ODBD=8，
∴所求图形面积为=8- ．

关闭