
【题目】如图所示,在![]() 的正方形网格中,从点
的正方形网格中,从点![]() 出发的四条线段
出发的四条线段![]() ,
,![]() ,
,![]() ,
,![]() ,它的另一个端点
,它的另一个端点![]() ,
,![]() ,
,![]() ,
,![]() 均在格点上(正方形网格的交点).
均在格点上(正方形网格的交点).

(1)若每个小正方形的边长都是1,分别求出![]() ,
,![]() ,
,![]() ,
,![]() 的长度(结果保留根号).
的长度(结果保留根号).
(2)在![]() ,
,![]() ,
,![]() ,
,![]() 四条线段中,是否存在三条线段,它们能构成直角三角形?如果存在,请指出是哪三条线段,并说明理由.
四条线段中,是否存在三条线段,它们能构成直角三角形?如果存在,请指出是哪三条线段,并说明理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在RtΔABC中,∠C=90°,∠BAC的角平分线AD交BC边于D,以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D,与AB边的另一个交点为E.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为4,∠B=30°.求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月18日晚,苏宁易购发布618全程战报:从6月1日到18日晚6点,苏宁依托线上线下全场景优势,逆势增长.经调查,苏宁易购线上有甲乙两家在销售华为A手机、华为B电脑和华为C耳机.已知每部A手机的利润率为40%,每台B电脑的利润率为60%,每副C耳机的利润率为30%,甲商家售出的B电脑和C耳机的数量都是A手机的数量的一半,获得的总利润为50%,乙商家售出的A手机的数量是B电脑的数量的一半,售出的C耳机的数量是B电脑的数量的![]() ,则乙商家获得的总利润率是___________.
,则乙商家获得的总利润率是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形A`B`C`是由三角形ABC经过某种平移得到的,点A与点A`,点B与点B`,点C与点C`分别对应,观察点与点坐标之间的关系,解答下列问题:

![]() 分别写出点A、点B、点C、点A`、点B`、点C`的坐标,并说明三角形A`B`C`是由三角形ABC经过怎样的平移得到的.
分别写出点A、点B、点C、点A`、点B`、点C`的坐标,并说明三角形A`B`C`是由三角形ABC经过怎样的平移得到的.
![]() 若点
若点![]() 是点
是点![]() 通过
通过![]() 中的平移变换得到的,求
中的平移变换得到的,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,∠1=75°,∠2=105°,∠C=∠D.判断 ∠A与 ∠F的大小关系,并说明理由.

(2)对于某些数学问题,灵活运用整体思想,可以化难为易.在解二元一次方程组时,就可以运用整体代入法:如解方程组: .
.
解:把②代入①得,![]() 解得
解得![]() 把
把![]() 代入②得,
代入②得,![]()
所以方程组的解为 ![]()
请用同样的方法解方程组: .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①b2-4ac>0;②2a+b<0;③4a-2b+c=0;④a∶b∶c=-1∶2∶3.其中正确的是( )
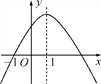
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究并解决问题:
探究
倍延三角形的一条中线,我们可以发现一些有用的结论.
已知,如图①所示,AD为△ABC的中线,延长AD到E,使AD=DE,连接BE、CE.
(1)求证:AB∥CE.

(2)请再写出两条不同类型的结论.
解决问题
如图所示②,分别以△ABC的边AB和AC为边,向三角形的外侧作两个等腰直角三角形,AB=AD,AC=AE,∠BAD = ∠CAE=90°,点M为BC的中点,连接DE,AM,试问线段AM、DE之间存在什么关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《函数的图象与性质》拓展学习片段展示:
【问题】
如图①,在平面直角坐标系中,抛物线y=a(x-2)2-4经过原点O,与x轴的另一个交点为A,则a= ,点A的坐标为 .
【操作】
将图①中的抛物线在x轴下方的部分沿x轴翻折到x轴上方,如图②.直接写出翻折后的这部分抛物线对应的函数解析式: .
【探究】
在图②中,翻折后的这部分图象与原抛物线剩余部分的图象组成了一个“W”形状的新图象,则新图象对应的函数y随x的增大而增大时,x的取值范围是 .
【应用】结合上面的操作与探究,继续思考:
如图③,若抛物线y=(x-h)2-4与x轴交于A,B两点(A在B左),将抛物线在x轴下方的部分沿x轴翻折,同样,也得到了一个“W”形状的新图象.
(1)求A、B两点的坐标;(用含h的式子表示)
(2)当1<x<2时,若新图象的函数值y随x的增大而增大,求h的取值范围.



查看答案和解析>>
科目:初中数学 来源: 题型:
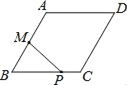
【题目】如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP 2=y,则表示y与x的函数关系的图象大致为( )
A. 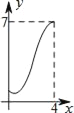 B.
B. 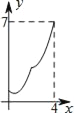 C.
C. 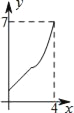 D.
D. 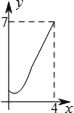
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com