
分析 根据方程x2+2ax+2a2-1=0至少有一个正根,则方程一定有两个实数根,即△≥0,关于x的方程x2+2ax+2a2-1=0至少有一个正根?(1)当方程有两个相等的正根,(2)当方程有两个不相等的根,①若方程的两个根中只有一个正根,一个负根或零根,②若方程有两个正根,结合二次方程的根的情况可求.
解答 解:△=(2a)2-4×1×(2a2-1)=-4a2+4,
(1)当方程有两个相等的正根时,△=0,此时a=±1,
若a=1,此时方程x2+2x+1=0的根x=-1不符合条件,舍去,
若a=-1,此时方程x2-2x+1=0的根x=1符合条件;
(2)当方程有两个根时,△>0可得-1<a<1,
①若方程的两个根中只有一个正根,一个负根或零根,则有2a2-1≤0,
解得:-$\frac{\sqrt{2}}{2}$≤a≤$\frac{\sqrt{2}}{2}$,
而a=$\frac{\sqrt{2}}{2}$时不合题意,舍去.
所以-$\frac{\sqrt{2}}{2}$≤a≤<$\frac{\sqrt{2}}{2}$符合条件;
②若方程有两个正根,则$\left\{\begin{array}{l}{-2a>0}\\{2{a}^{2}-1>0}\end{array}\right.$,
解得:a<-$\frac{\sqrt{2}}{2}$,
综上,-1≤a<$\frac{\sqrt{2}}{2}$,
故答案为:-1≤a<$\frac{\sqrt{2}}{2}$.
点评 本题考查了一元二次方程根的判别式的应用以及一元二次方程根的应用,熟练掌握根的判别式及分类讨论思想的运用是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
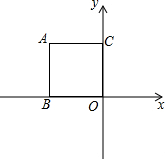 如图,在平面直角坐标系中,已知A(-8,8),B(-8,0),C(0,8),连结AB,AC,若画出含边长为5的等腰三角形,A为顶角的顶点,另外两个顶点在折线AB-BO-OC-CA上,则等腰三角形的面积为$\frac{5}{2}$或20$\sqrt{2}$-$\frac{25}{4}$.
如图,在平面直角坐标系中,已知A(-8,8),B(-8,0),C(0,8),连结AB,AC,若画出含边长为5的等腰三角形,A为顶角的顶点,另外两个顶点在折线AB-BO-OC-CA上,则等腰三角形的面积为$\frac{5}{2}$或20$\sqrt{2}$-$\frac{25}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-7)×$\frac{4}{3}$×(-2.5) | B. | (-7)×(-$\frac{4}{3}$)×(-2.5) | C. | (-7)×(-$\frac{4}{3}$)×(-$\frac{2}{5}$) | D. | (-7)×(-$\frac{3}{4}$)×(-$\frac{5}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com