
【题目】教材呈现:下图是华师版九年级上册数学教材第77页的部分内容.
猜想:

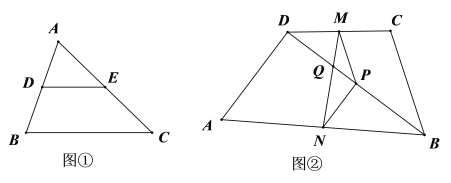
如图,在![]() 中,点
中,点![]() 分别是
分别是![]() 与
与![]() 的中点,根据画出的图形,可以猜想:
的中点,根据画出的图形,可以猜想:
![]() ,且
,且![]() .
.
对此,我们可以用演绎推理给出证明.
证明:在![]() 中,
中,
∵点![]() 分别是
分别是![]() 与
与![]() 的中点,
的中点,
∴![]() .
.
请根据教材提示,结合图①,写出完整的证明过程.
结论应用:
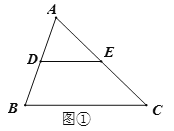
如图②在四边形![]() 中,
中,![]() ,点
,点![]() 是对角线
是对角线![]() 的中点,
的中点,![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点,
中点,![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,则
,则![]() _______________.
_______________.
【答案】猜想:证明过程见解析;结论应用:(1)见解析;(2)![]() .
.
【解析】
猜想:利用两边对应成比例且夹角相等可证![]() ,再利用相似三角形的性质即可证得猜想;
,再利用相似三角形的性质即可证得猜想;
结论应用:(1)根据猜想的结论可得:![]() ,
,![]() ,进而可得
,进而可得![]() ,然后利用等腰三角形的性质即可得出结论;
,然后利用等腰三角形的性质即可得出结论;
(2)过点P作PF⊥MN于点F,如图②,由(1)得:PN∥AD,PM∥BC,然后利用平行线的性质即可求出∠MPN,再由(1)的结论可得∠2的度数,因为![]() ,而BC=4,所以MP=2,因为∠PQF=∠1+∠2,所以∠PQF可得,然后在直角△PQF中利用30°角的直角三角形的性质即可求出结果.
,而BC=4,所以MP=2,因为∠PQF=∠1+∠2,所以∠PQF可得,然后在直角△PQF中利用30°角的直角三角形的性质即可求出结果.
教材呈现:
证明:在![]() 中,∵点
中,∵点![]() 分别是
分别是![]() 与
与![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
结论应用:
(1)证明:∵![]() 分别为
分别为![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() 分别为
分别为![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ;
;
(2)解:过点P作PF⊥MN于点F,如图②,
由(1)得:PN∥AD,PM∥BC,
∴∠NPB=∠ADB=90°=∠NPD,∠1=∠DBC=30°,∴∠MPN=30°+90°=120°,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴PF=![]() ,
,
∵∠PQF=∠1+∠2=60°,∴∠QPF=30°,
∴![]() ,
,
∴![]()
![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】某公司生产一种节能型灯具并加以销售,现准备在甲市和乙市按不同的方案进行销售,若只在甲市销售,销售价为![]() (元/件),月销售量为
(元/件),月销售量为![]() (件),
(件),![]() 是
是![]() 的一次函数.如表所示,成本为50元/件,无论销售多少,每月还需支出广告费用72500元。设月利润为
的一次函数.如表所示,成本为50元/件,无论销售多少,每月还需支出广告费用72500元。设月利润为![]() (元),(利润=销售额-成本-广告费).若只在乙市销售,销售价为200元/件,受各种因素影响,成本为
(元),(利润=销售额-成本-广告费).若只在乙市销售,销售价为200元/件,受各种因素影响,成本为![]() 元/件(
元/件(![]() 为常数且
为常数且![]() ),当月销售量为
),当月销售量为![]() 件时,每月还需交纳
件时,每月还需交纳![]() 的附加费,设月利润为
的附加费,设月利润为![]() (元).(利润=销售额-成本-附加费)
(元).(利润=销售额-成本-附加费)
月销售量 | 1500 | 2000 |
销售价格 | 185 | 180 |
(1)当![]() 时,
时,![]() ______元/件,
______元/件,![]() ______元(直接写出结果).
______元(直接写出结果).
(2)分别求出![]() 、
、![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的取值范围).
的取值范围).
(3)当![]() 为何值时,
为何值时,![]() 最大?若在乙市销售月利润最大值与甲市最大值相同,求
最大?若在乙市销售月利润最大值与甲市最大值相同,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为xm,窗户的透光面积为ym2(铝合金条的宽度不计).
(1)求出y与x的函数关系式;
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晓东在解一元二次方程时,发现有这样一种解法:
如:解方程![]() .
.
解:原方程可变形,得
![]() .
.
![]() ,
,
![]() ,
,
![]()
直接开平方并整理,得![]() ,
,![]() .
.
我们称晓东这种解法为“平均数法”.
(1)下面是晓东用“平均数法”解方程![]() 时写的解题过程.
时写的解题过程.
![]() .
.
![]() ,
,
![]() .
.
直接开平方并整理,得![]() ,
,![]() .
.
上述过程中的“□”,“○”,“☆”,“¤”表示的数分别为________,________,________,________.
(2)请用“平均数法”解方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
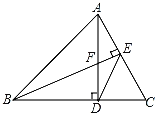
【题目】如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F,连接ED.
(1)求证:△AEF∽△BDF;
(2)若AE=4,BD=8,EF+DF=9,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
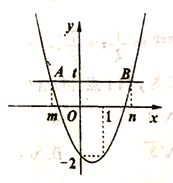
【题目】如图为二次函数![]() 图象,直线
图象,直线![]() 与抛物线交于
与抛物线交于![]() 两点,
两点,![]() 两点横坐标分别为
两点横坐标分别为![]() 根据函数图象信息有下列结论:
根据函数图象信息有下列结论:
①![]() ;
;
②若对于![]() 的任意值都有
的任意值都有![]() ,则
,则![]() ;
;
③![]() ;
;
④![]() ;
;
⑤当![]() 为定值时若
为定值时若![]() 变大,则线段
变大,则线段![]() 变长
变长
其中,正确的结论有__________(写出所有正确结论的番号)
查看答案和解析>>
科目:初中数学 来源: 题型:
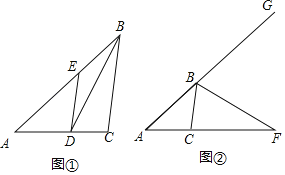
【题目】探究:如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥BC交AB于点E,AB=5,BC=3,求![]() 的值.
的值.
应用:如图②,在△ABC中,BF是△ABC的外角的平分线,交AC的延长线于点F,AB=5,BC=3,则![]() =______.
=______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com