
【题目】如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2). 把一根长为2015个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )

A. (1,-1) B. (-1,1) C. (-1,-2) D. (1,-2)
科目:初中数学 来源: 题型:
【题目】为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手.
(1)一条直线把平面分成2部分;
(2)两条直线最多可把平面分成4部分;
(3)三条直线最多可把平面分成7部分…
把上述探究的结果进行整理,列表如下:
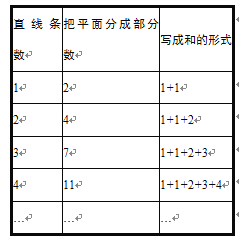
(1)当直线条数为5时,把平面最多分成 部分,写成和的形式为 ;
(2)当直线条数为10时,把平面最多分成 部分;
(3)当直线条数为n时,把平面最多分成几部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】景区大楼AB段上有四处居民小区A,B,C,D,且有AC=CD=DB,为改善居民购物的环境,要在AB路建一家超市,每个小区的居民各执一词,难以确定超市的位置,如果由你出任超市负责人,以便民、获利的角度考虑,你将把超市建在哪儿?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
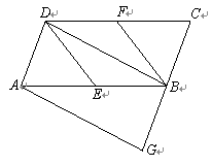
【题目】如图,在□ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于函数y=2x , 下列结论中正确的是( )
A.函数图象都经过点(2,1)
B.函数图象都经过第二、四象限
C.y随x的增大而增大
D.不论x取何值,总有y>0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com