
【题目】如图,抛物线 ![]() 经过点
经过点 ![]() ,交y 轴于点C:
,交y 轴于点C:
(1)求抛物线的解析式(用一般式表示).
(2)点 ![]() 为
为 ![]() 轴右侧抛物线上一点,是否存在点
轴右侧抛物线上一点,是否存在点 ![]() 使
使 ![]() ,若存在请直接给出点
,若存在请直接给出点 ![]() 坐标;若不存在请说明理由.
坐标;若不存在请说明理由.
(3)将直线 ![]() 绕点
绕点 ![]() 顺时针旋转
顺时针旋转 ![]() ,与抛物线交于另一点
,与抛物线交于另一点 ![]() ,求
,求 ![]() 的长.
的长.
【答案】
(1)
解:依题可得:![]()
解得:
∴y=-![]() x2+
x2+![]() x+2.
x+2.
(2)
解:依题可得:AB=5,OC=2,
∴S△ABC=![]() AB×OC=
AB×OC=![]() ×2×5=5.
×2×5=5.
∵S△ABC=![]() S△ABD.
S△ABD.
∴S△ABD=![]() ×5=
×5=![]() .
.
设D(m,-![]() m2+
m2+![]() m+2)(m>0).
m+2)(m>0).
∵S△ABD=![]() AB|yD|=
AB|yD|=![]() .|
.|
![]() ×5×|-
×5×|-![]() m2+
m2+![]() m+2|=
m+2|=![]() .
.
∴m=1或m=2或m=-2(舍去)或m=5
∴D1(1,3),D2(2,3),D3(5,-3).
(3)
解:过C作CF⊥BC交BE于点F;过点F作FH⊥y轴于点H.
∵∠CBF=45°,∠BCF=90°.
∴CF=CB.
∵∠BCF=90°,∠FHC=90°.
∴∠HCF+∠BCO=90°,∠HCF+∠HFC=90°
∴∠HFC=∠OCB.
∵
∴△CHF≌△BOC(AAS).
∴HF=OC=2,HC=BO=4,
∴F(2,6).
设直线BE解析式为y=kx+b.
∴![]()
解得![]()
∴直线BE解析式为:y=-3x+12.
∴
解得:x1=5,x2=4(舍去)
∴E(5,-3).
BE=![]() =
=![]() .
.

【解析】(1)用待定系数法求二次函数解析式.
(2)依题可得:AB=5,OC=2,求出S△ABC=![]() AB×OC=
AB×OC=![]() ×2×5=5;根据S△ABC=
×2×5=5;根据S△ABC=![]() S△ABD;求出S△ABD=
S△ABD;求出S△ABD=![]() ×5=
×5=![]() .
.
设D(m,-![]() m2+
m2+![]() m+2)(m>0).根据三角形的面积公式得到一个关于m的方程,求解即可.
m+2)(m>0).根据三角形的面积公式得到一个关于m的方程,求解即可.
(3)过C作CF⊥BC交BE于点F;过点F作FH⊥y轴于点H;根据同角的余角相等得到∠HFC=∠OCB;再根据条件得到△CHF≌△BOC(AAS);利用其性质可求出HF=OC=2,HC=BO=4,从而得到F(2,6);用待定系数法求直线BE解析式;再把抛物线解析式和直线BE解析式联立得到方程组求E点坐标,再根据勾股定理求出BE长.
【考点精析】本题主要考查了因式分解法和确定一次函数的表达式的相关知识点,需要掌握已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势;确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】某电器公司计划装运甲、乙、丙三种家电到农村销售(规定每辆汽车按规定满载,且每辆汽车只能装同一种家电).下表所示为装运甲、乙、丙三种家电的台数及利润.
甲 | 乙 | 丙 | |
每辆汽车能装运的台数 | 40 | 20 | 30 |
每台家电可获利润(万元) | 0.05 | 0.07 | 0.04 |
(1)若用8辆汽车装运乙、丙两种家电190台到A地销售,问装运乙、丙的汽车各多少辆.
(2)计划用20辆汽车装运甲、乙、丙三种家电720台到B地销售,如何安排装运,可使公司获得36.6万元的利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,河坝横断面背水坡AB的坡角是45°,背水坡AB长度为20 ![]() 米,现在为加固堤坝,将斜坡AB改成坡度为1:2的斜坡AD【备注:AC⊥CB】
米,现在为加固堤坝,将斜坡AB改成坡度为1:2的斜坡AD【备注:AC⊥CB】 
(1)求加固部分即△ABD的横截面的面积;
(2)若该堤坝的长度为100米,某工程队承包了这一加固的土石方工程,为抢在在汛期到来之际提前完成这一工程,现在每天完成的土方比原计划增加25%,这样实际比原计划提前10天完成了,求原计划每天完成的土方.【提示土石方=横截面x堤坝长度】
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表列出了国外几个城市与首都北京的时差(带正号的表示同一时刻比北京时间早的时数),如北京时间的上午10:00时,东京时间的10点已过去了1小时,现在已是10+1=11:00.
(1)如果现在是北京时间下午3:00,那么现在的纽约时间是多少?
(2)此时(北京时间9:00)小明想给远在巴黎的姑妈打电话,你认为合适吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
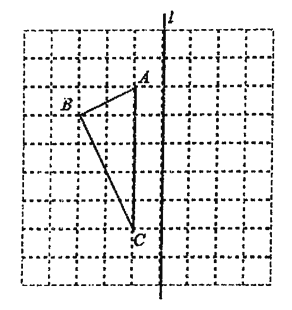
【题目】如图,正方形网格中每个小正方形边长都是1.
(1)画出△ABC关于直线1对称的图形△A1BlCl;
(2)在直线l上找一点P,使PB=PC;(要求在直线1上标出点P的位置)
(3)连接PA、PC,计算四边形PABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AD是△ABC的中线,∠ACE是△ABC的外角. 
(1)读下列语句,尺规作图,保留作图痕迹. ①作∠ACE的角平分线,交BA延长线于点F;
②过点D作DH∥AC,交AB于点H,连接CH.
(2)依据以上条件,解答下列问题. ①与△AHD面积相等的三角形是;
②若∠B=40°,∠F=30°,求∠BAC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com