

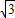 t,根据三角形的面积公式即可得出S,t的函数关系式.
t,根据三角形的面积公式即可得出S,t的函数关系式. .
. ),B(6,2
),B(6,2 ).(3分)
).(3分)
 t.
t. ON•MN=
ON•MN= t2.(4分)
t2.(4分)
 ON•MN=
ON•MN= ×t×2
×t×2 =
= t.(6分)
t.(6分)
 -
- (t-4)=6
(t-4)=6 -
- t,
t, OH•MN=
OH•MN= t(6
t(6 -
- t)
t) t2+3
t2+3 t.
t. ×22=2
×22=2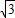 ,
, ,
, (t-3)2+
(t-3)2+ ,
, t2+3
t2+3 t的最大值是
t的最大值是 .
. t2+3
t2+3 t的最大值不是
t的最大值不是 .
. t2+3
t2+3 t随t的增大而减小,
t随t的增大而减小, .
. .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2006年全国中考数学试题汇编《平面直角坐标系》(02)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2006年辽宁省锦州市中考数学试卷(解析版) 题型:解答题
 (2006•锦州)如图,△ABC是等腰直角三角形,其中CA=CB,四边形CDEF是正方形,连接AF、BD.
(2006•锦州)如图,△ABC是等腰直角三角形,其中CA=CB,四边形CDEF是正方形,连接AF、BD.查看答案和解析>>
科目:初中数学 来源:2006年辽宁省锦州市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2006年辽宁省锦州市中考数学试卷(解析版) 题型:填空题
 (AD+BC)=
(AD+BC)= (a+b);
(a+b); (E1F1+BC)=
(E1F1+BC)= [
[ (a+b)+b]=
(a+b)+b]= (a+3b);当E3,F3分别是E2B,F2C的中点,则E3F3=
(a+3b);当E3,F3分别是E2B,F2C的中点,则E3F3= (E2F2+BC)=
(E2F2+BC)= (a+7b);若EnFn分别是En-1,Fn-1的中点,根据上述规律猜想EnFn= .(n≥1,n为整数)
(a+7b);若EnFn分别是En-1,Fn-1的中点,根据上述规律猜想EnFn= .(n≥1,n为整数)
查看答案和解析>>
科目:初中数学 来源:2006年辽宁省锦州市中考数学试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com