
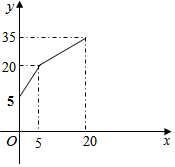
 一个水槽有进水管和出水管各一个,进水管每分钟进水m升,出水管每分钟出水n升,水槽在开始5分钟内只进水不出水,随后15分钟内既进水又出水,得到时间x(分)与水量y(升)之间的关系如图所示:
一个水槽有进水管和出水管各一个,进水管每分钟进水m升,出水管每分钟出水n升,水槽在开始5分钟内只进水不出水,随后15分钟内既进水又出水,得到时间x(分)与水量y(升)之间的关系如图所示:分析 (1)根据“每分钟进水量=进水总量÷进水时间”即可求出m的值,再根据“每分钟出水量=每分钟进水量-进水总量÷进水时间”即可求出n值;
(2)根据“水槽水量=35升-每分钟出水量×放水时间”即可得出y关于x的函数解析式,令y=0求出x值,由此即可得出定义域,将该段函数图象在图形上补充完整即可.
解答 解:(1)进水管每分钟进水量为:(20-5)÷5=3(升);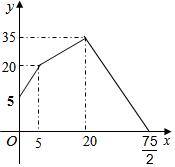
出水管每分钟出水量为:3-(35-20)÷(20-15)=2(升).
∴m的值为3,n的值为2.
(2)根据题意,得:y=35-2(x-20)=-2x+75,
当y=0时,有-2x+75=0,
解得:x=$\frac{75}{2}$,
∴20分钟后y关于x的函数解析式为y=-2x+75(20<x≤$\frac{75}{2}$),将图形补充完整如图所示.
点评 本题考查了一次函数的应用,根据数量关系找出y关于x的函数关系式是解题的关键.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:选择题
| A. | 1米 | B. | 2米 | C. | 4米 | D. | 5米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
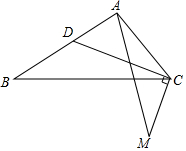 如图,△ABC中,∠ACB=α(0°<α<90°),CD平分∠ACB,过C点作CD的垂线交AB的垂直平分线于M,连接AM,求∠BAM(用含α的式子表示).
如图,△ABC中,∠ACB=α(0°<α<90°),CD平分∠ACB,过C点作CD的垂线交AB的垂直平分线于M,连接AM,求∠BAM(用含α的式子表示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com