
【题目】如图,已知直线![]() ,
,![]() 分别是直线
分别是直线![]() 上的点.
上的点.
(1)在图1中,判断![]() 和
和![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(2)在图2中,请你直接写出![]() 和
和![]() 之间的数量关系(不需要证明);
之间的数量关系(不需要证明);
(3)在图3中,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)![]() ,证明见析;(2)
,证明见析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)如图,过点![]() 作直线
作直线![]() ,由平行线的性质得到
,由平行线的性质得到![]() ,
,![]() ,即可求得
,即可求得![]() ;
;
(2)如图,记AB与NE的交点为G,由平行线的性质得∠EGM=∠DNE,由三角形外角性质得∠BME=∠MEN+∠EGM,由此即可得到结论;
(3)由角平分线的定义设![]() ,设
,设![]() ,由(1),得
,由(1),得![]() ,由(2),得
,由(2),得![]() ,再根据
,再根据![]() ,可求得
,可求得![]() ,继而可求得
,继而可求得![]() .
.
(1)![]() ,证明如下:
,证明如下:
如图,过点![]() 作直线
作直线![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;

(2)![]() ,理由如下:
,理由如下:
如图,记AB与NE的交点为G,
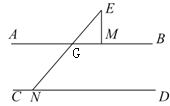
又∵AB//CD,
∴∠EGM=∠DNE,
∵∠BME是△EMG的外角,
∴∠BME=∠MEN+∠EGM,
∴∠MEN=∠BME-∠DNE;
(3)∵![]() 平分
平分![]() ,
,
∴设![]() ,
,
∵![]() 平分
平分![]() ,
,
∴设![]() ,
,
由(1),得![]() ,
,
由(2),得![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】一副三角板如图摆放,点F是 45°角三角板△ABC的斜边的中点,AC=4.当 30°角三角板DEF的直角顶点绕着点F旋转时,直角边DF,EF分别与AC,BC相交于点 M, N.在旋转过程中有以下结论:①MF=NF;②CF与MN可能相等吗;③MN 长度的最小值为 2;④四边形CMFN的面积保持不变; ⑤△CMN面积的最大值为 2.其中正确的个数是_________.(填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民选购家用净水器.我市飞龙商场抓住商机,从厂家购进了A、B两种型号家用净水器共100台,A型号家用净水器进价是150元/台,B型号家用净水器进价是250元/台,购进两种型号的家用净水器共用去19000 元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这100台家用净水器的毛利润不低于5600元,求每台A型号家用净水器的售价至少是多少元? (注: 毛利润=售价一进价) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3 在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.

原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)思路梳理
∵AB=CD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线.
根据___________,SAS
易证△AFG≌___________△AEF
,得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°.点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系______________∠B+∠D=180°
时,仍有EF=BE+DF.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°.猜想BD、DE、EC应满足的等量关系,并写出推理过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把1°的圆心角所对的弧叫做1°的弧,则圆心角AOB的度数等于它所对的弧AB的度数记为:∠AOB![]()
![]() .由此可知:命题“圆周角的度数等于其所对的弧的度数的一半.”是真命题,请结合图形1给予证明(不要求写已知、求证,只需直接证明),并解决以下的问题(1)和问题(2).
.由此可知:命题“圆周角的度数等于其所对的弧的度数的一半.”是真命题,请结合图形1给予证明(不要求写已知、求证,只需直接证明),并解决以下的问题(1)和问题(2).
问题(1):如图2,⊙O的两条弦AB、CD相交于圆内一点P,求证:∠APC![]()
![]() (
(![]() +
+![]() );
);
问题(2):如图3,⊙O的两条弦AB、CD相交于圆外一点P,问题(1)中的结论是否成立,如果成立,给予证明;如果不成立,写出一个类似的结论(不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() (四边相等,四个角都是直角),点
(四边相等,四个角都是直角),点![]() 为边
为边![]() 上异于点
上异于点![]() 的一动点,
的一动点,![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 延长线上一定点,满足
延长线上一定点,满足![]() ,
,![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
(1)判断![]() 是 三角形.
是 三角形.
(2)求证: ![]() ≌
≌![]() .
.
(3)探究![]() 是否为定值?如果是定值,请说明理由,并求出该定值;如果不是定值,请说明理由.
是否为定值?如果是定值,请说明理由,并求出该定值;如果不是定值,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
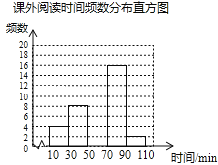
【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如下不完整的统计表.
课外阅读时间t | 频数 | 百分比 |
10≤t<30 | 4 | 8% |
30≤t<50 | 8 | 16% |
50≤t<70 | a | 40% |
70≤t<90 | 16 | b |
90≤t<110 | 2 | 4% |
合计 | 50 | 100% |
请根据图表中提供的信息回答下列问题:
(1)a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若全校有900名学生,估计该校有多少学生平均每天的课外阅读时间不少于50min?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com