
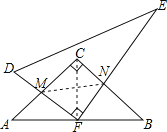
【题目】一副三角板如图摆放,点F是 45°角三角板△ABC的斜边的中点,AC=4.当 30°角三角板DEF的直角顶点绕着点F旋转时,直角边DF,EF分别与AC,BC相交于点 M, N.在旋转过程中有以下结论:①MF=NF;②CF与MN可能相等吗;③MN 长度的最小值为 2;④四边形CMFN的面积保持不变; ⑤△CMN面积的最大值为 2.其中正确的个数是_________.(填写序号).

【答案】①②④⑤
【解析】
利用两直角三角形的特殊角、性质及旋转的性质分别判断每一个结论,找到正确的即可.
解:①连接CF,
∵F为AB中点,AC=BC,∠ACB=90°,
∴AF=BF=CF,CF⊥AB,
∴∠AFM+∠CFM=90°.
∵∠DFE=90°,∠CFM+∠CFN=90°,
∴∠AFM=∠CFN.
同理,∵∠A+∠MCF=90°,∠MCF+∠FCN=90°,
∴∠A=∠FCN,
在△AMF与△CNF中,
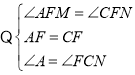
∴△AMF≌△CNF(ASA),
∴MF=NF.
故①正确;
∴②∵F是AB中点,△ABC是等腰直角三角形,![]() ,
,
当M,N分别是AC,BC中点时,![]() ,
,
CF=MN,故正确;
③连接MN,当M为AC的中点时,CM=CN,根据边长为4知CM=CN=2,此时MN最小,最小值为![]() ,故③错误;
,故③错误;
④当M、N分别为AC、BC中点时,四边形CMFN是正方形.
∵△AMF≌△CNF,
∴S△AMF=S△CNF
∴S四边形CDFE=S△AFC.
故④正确;
⑤由于△MNF是等腰直角三角形,因此当FM最小时,FN也最小;
即当DF⊥AC时,FM最小,此时![]() ,
,
![]() ,
,
当△CMN面积最大时,此时△FMN的面积最小.
此时S△CMN=S四边形CMFN-S△FMN=S△AFC-S△FMN=4-2=2,
故⑤正确.


科目:初中数学 来源: 题型:
【题目】某商场购进一批LED灯泡与普通白炽灯炮,其进价与标价如下表,该商场购进LED灯泡与普通白炽灯炮共300个,LED灯泡按标价进行销售,而普通白炽灯炮按标价打九折销售,销售完这批灯泡后可以获利3200元。
(1)求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进两种灯泡120个,并在不打折的情况下销售完,若销售完这批灯泡的获利不超过总进货价的28%,则最多购进LED灯泡多少个?
LED灯泡 | 普通白炽灯泡 | |
进价(元) | 45 | 25 |
标价(元) | 60 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).
(1)求直线AB的解析式及抛物线y=ax2的解析式;
(2)求点C的坐标;
(3)求S△COB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+1的图象与x轴、y轴分别交于A、B两点,将这条直线进行平移后交x轴、y轴分别交于C、D,要使A、B、C、D围成的四边形面积为4,则直线CD的解析式为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象经过点A(1,3).
的图象经过点A(1,3).
(1)试确定此反比例函数的解析式;
(2)当![]() =2时, 求y的值;
=2时, 求y的值;
(3)当自变量![]() 从5增大到8时,函数值y是怎样变化的?
从5增大到8时,函数值y是怎样变化的?
查看答案和解析>>
科目:初中数学 来源: 题型:
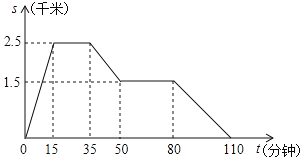
【题目】一天,王亮同学从家里跑步到体育馆,在那里锻炼了一阵后又走到某书店去买书, 然后散步走回家如图反映的是在这一过程中,王亮同学离家的距离 s(千米)与离家的时间 t(分钟)之间的关系,请根据图象解答下列问题:
(1)体育馆离家的距离为 千米,书店离家的距离为_____千米;王亮同学在书店待了______分钟.
(2)分别求王亮同学从体育馆走到书店的平均速度和从书店出来散步回家的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形的是( )
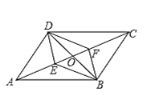
A. AE=CFB. DE=BF
C. ∠ADE=∠CBFD. ∠ABE=∠CDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() ,
,![]() 分别是直线
分别是直线![]() 上的点.
上的点.
(1)在图1中,判断![]() 和
和![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(2)在图2中,请你直接写出![]() 和
和![]() 之间的数量关系(不需要证明);
之间的数量关系(不需要证明);
(3)在图3中,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com