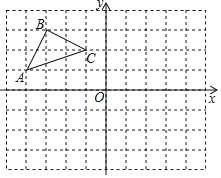
[题目]按要求完成作图:(1)作出△ABC关于x轴对称的图形,(2)写出A.B.C的对应点A′.B′.C′的坐标,(3)直接写出△ABC的面积．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】按要求完成作图：

（1）作出△ABC关于x轴对称的图形；

（2）写出A、B、C的对应点A′、B′、C′的坐标；

（3）直接写出△ABC的面积　　．

【答案】（1）见解析（2）A′（﹣4，﹣1）、B′（﹣3，﹣3）、C′（﹣1，﹣2）（3）2.5

【解析】

（1）依据轴对称的性质，即可得到△ABC关于x轴对称的图形；

（2）依据对应点A′、B′、C′的位置，即可得到其坐标；

（3）依据割补法进行计算，即可得到△ABC的面积．

解：（1）如图所示，△A'B'C'即为所求；

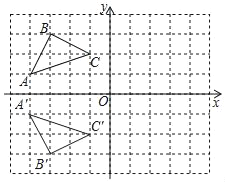
（2）由图可得，A′（﹣4，﹣1）、B′（﹣3，﹣3）、C′（﹣1，﹣2）；

（3）△ABC的面积＝2×3﹣×1×2﹣×1×2﹣×1×3＝6﹣1﹣1﹣1.5＝2.5．

故答案为：（1）见解析；（2）A′（﹣4，﹣1）、B′（﹣3，﹣3）、C′（﹣1，﹣2）；

（3）2.5．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，在中，，，为上一个动点，过点作交折线于点，设的长为，的面积为，关于函数图象，两段组成，如图所示．

（）当时，求的长．

（）求图中的图象段的函数解析式．

（）求为何值时，的面积为．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，ABCD中，M、N是BD的三等分点，连接CM并延长交AB于点E，连接EN并延长交CD于点F，以下结论：

①E为AB的中点；

②FC=4DF；

③S△ECF=；

④当CE⊥BD时，△DFN是等腰三角形．

其中一定正确的是_____．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】一副三角板如图摆放，点F是 45°角三角板△ABC的斜边的中点，AC＝4．当 30°角三角板DEF的直角顶点绕着点F旋转时，直角边DF，EF分别与AC，BC相交于点 M， N．在旋转过程中有以下结论：①MF＝NF；②CF与MN可能相等吗；③MN 长度的最小值为 2；④四边形CMFN的面积保持不变； ⑤△CMN面积的最大值为 2．其中正确的个数是_________.（填写序号）.