
| 污水处理设备 | A型 | B型 |
| 价格(万元/台) | m | m-3 |
| 月处理污水量(吨/台) | 220 | 180 |
| 90 |
| m |
| 75 |
| m-3 |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
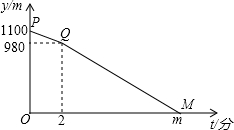 A,B两地相距1100米,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2分钟,乙出发7分钟后与甲相遇.设甲、乙两人相距y米,甲行进的时间为t分钟,y与t之间的函数关系如图所示.请你结合图象探究:
A,B两地相距1100米,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2分钟,乙出发7分钟后与甲相遇.设甲、乙两人相距y米,甲行进的时间为t分钟,y与t之间的函数关系如图所示.请你结合图象探究:查看答案和解析>>
科目:初中数学 来源: 题型:
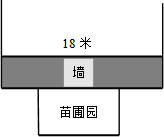 大陇初级中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成.如图已知墙长为18米,设这个苗圃园垂直于墙的一边的长为x米.
大陇初级中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成.如图已知墙长为18米,设这个苗圃园垂直于墙的一边的长为x米.查看答案和解析>>
科目:初中数学 来源: 题型:
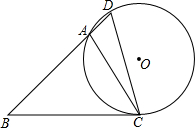 如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3
如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com