
分析 (1)12+22+32+42+52=$\frac{5×6×11}{6}$
(2)12+22+32…+n2=$\frac{n(n+1)(2n+1)}{6}$
(3)先算出:12+22+32…+502与12+22+32…+512+522+…+992+1002的值,再求它们的差即可
解答 解:(1)12+22+32+42+52=$\frac{5×6×11}{6}$
(2)12+22+32…+n2=$\frac{n(n+1)(2n+1)}{6}$
(3∵12+22+32…+502=$\frac{50×51×101}{6}$=42925
12+22+32…+512+522+…+992+1002=$\frac{100×101×201}{6}$=338350
∴512+522+…+992+1002=(12+22+32…+512+522+…+992+1002)-(12+22+32…+502)
=338350-42925
=295425
故答案为:①=$\frac{5×6×11}{6}$;②=$\frac{n(n+1)(2n+1)}{6}$;③295425
点评 本题考查了数字的变化规律问题,解题的关键是认真阅读题目中数字变化的规律,难点是512+522+…+992+1002=(12+22+32…+512+522+…+992+1002)-(12+22+32…+502)的变形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
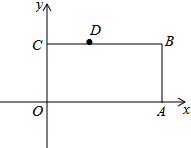 如图,已知长方形OABC的两边分别在x轴、y轴的正半轴上,且点A(4,0),一反比例函数y=$\frac{k}{x}$的图象与边BC交于点D(1,2)
如图,已知长方形OABC的两边分别在x轴、y轴的正半轴上,且点A(4,0),一反比例函数y=$\frac{k}{x}$的图象与边BC交于点D(1,2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com