
(8分)如图,在△ABC中,AB=AC,点O为底边上的中点,以点O为圆心,1为半径的半圆与边AB相切于点D.

1.(1)判断直线AC与⊙O的位置关系,并说明理由;
2.(2)当∠A=60°时,求图中阴影部分的面积.
1.解:(1)直线AC与⊙O相切.···················································································· 1分
理由是:
连接OD,过点O作OE⊥AC,垂足为点E.
∵⊙O与边AB相切于点D,
∴OD⊥AB.·················································································································· 2分
∵AB=AC,点O为底边上的中点,
∴AO平分∠BAC············································································································· 3分
又∵OD⊥AB,OE⊥AC
∴OD= OE······················································································································· 4分
∴OE是⊙O的半径.
又∵OE⊥AC,∴直线AC与⊙O相切.··········································································· 5分
2.(2)∵AO平分∠BAC,且∠BAC=60°,∴∠OAD=∠OAE=30°,
∴∠AOD=∠AOE=60°,
在Rt△OAD中,∵tan∠OAD = ,∴AD==![]() ,同理可得AE=
,同理可得AE=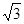
∴S四边形ADOE =×OD×AD×2=×1×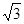 ×2=
×2=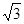 ························································· 6分
························································· 6分
又∵S扇形形ODE==π·························································································· 7分
∴S阴影= S四边形ADOE -S扇形形ODE=-π.······································································· 8分
解析:略


科目:初中数学 来源: 题型:
 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为A、
| ||||
B、(
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com