
如图,抛物线y=ax2﹣4和y=﹣ax2+4都经过x轴上的A、B两点,两条抛物线的顶点分别为C、D.当四边形ACBD的面积为40时,a的值为 .
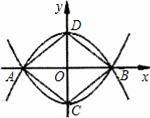

0.16【考点】二次函数综合题.
【专题】代数几何综合题;压轴题.
【分析】根据抛物线的解析式求得点A、B、C、D的坐标;然后求得以a表示的AB、CD的距离;最后根据三角形的面积公式求得S四边形ABCD=S△ABD+S△ABC,列出关于a的方程,通过解方程求得a值即可.
【解答】解:∵抛物线y=ax2﹣4和y=﹣ax2+4都经过x轴上的A、B两点,
∴点A、B两点的坐标分别是:(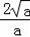
 ,0)、(﹣
,0)、(﹣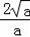
 ,0);
,0);
又∵抛物线y=ax2﹣4和y=﹣ax2+4的顶点分别为C、D.
∴点C、D的坐标分别是(0,4)、(0,﹣4);
∴CD=8,AB=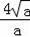
 ,
,
∴S四边形ABCD=S△ABD+S△ABC=
 AB•OD+
AB•OD+
 AB•OC
AB•OC
=
 AB•CD
AB•CD
=
 ×8×
×8×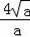
 =40,即
=40,即
 ×8×
×8×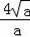
 =40,
=40,
解得,a=0.16;
故答案是:0.16.
【点评】本题考查了二次函数的综合题.解得该题时,须牢记:函数与x轴的交点的纵坐标是0,与y轴的交点的横坐标是0.


科目:初中数学 来源: 题型:
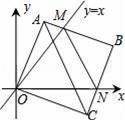
在平面直角坐标系中,边长为3的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).在旋转正方形OABC的过程中,△MBN的周长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法正确的是 ( )
A.为了了解某中学800名学生的视力情况,从中随机抽取了50名学生进行调查,在此次调查中,样本容量为50名学生的视力
B.若一个游戏的中奖率是1%,则做100次这样的游戏一定会中奖
C.了解无锡市每天的流动人口数,采用抽查方式
D.“掷一枚硬币,正面朝上”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
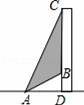
如图,某高楼CD与处地面垂直,要在高楼前的地面A处安装某种射灯,安装后,射灯发出的光线与地面的最大夹角∠DAC为70°,光线与地面的最小夹角∠DAB为35°,要使射灯发光时照射在高楼上的区域宽BC为50米,求A处到高楼的距离AD.(结果精确到0.1米)
【参考数据:sin70°=0.94,cos70°=0.34,tan70°=2.75,sin35°=0.57,cos35°=0.82,tan35°=0.70】

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com