
【题目】如图,港口B位于港口A的南偏东37°方向,灯塔C恰好在AB的中点处,一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行5km到达E处,测得灯塔C在北偏东45°方向上,这时,E处距离港口A有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
【答案】解:如图作CH⊥AD于H.设CH=xkm,
在Rt△ACH中,∠A=37°,∵tan37°= ![]() ,
,
∴AH= ![]() =
= ![]() ,
,
在Rt△CEH中,∵∠CEH=45°,
∴CH=EH=x,
∵CH⊥AD,BD⊥AD,
∴CH∥BD,
∴ ![]() =
= ![]() ,
,
∵AC=CB,
∴AH=HD,
∴ ![]() =x+5,
=x+5,
∴x= ![]() ≈15,
≈15,
∴AE=AH+HE= ![]() +15≈35km,
+15≈35km,
∴E处距离港口A有35km.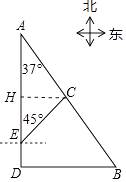
【解析】如图作CH⊥AD于H.设CH=xkm,在Rt△ACH中,可得AH= ![]() =
= ![]() ,在Rt△CEH中,可得CH=EH=x,由CH∥BD,推出
,在Rt△CEH中,可得CH=EH=x,由CH∥BD,推出 ![]() =
= ![]() ,由AC=CB,推出AH=HD,可得
,由AC=CB,推出AH=HD,可得 ![]() =x+5,求出x即可解决问题.
=x+5,求出x即可解决问题.
【考点精析】关于本题考查的关于方向角问题,需要了解指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
A种产品 | B种产品 | |
成本(万元∕件) | 3 | 5 |
利润(万元∕件) | 1 | 2 |
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)条件下,哪种方案获利最大?并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE. 
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强与小刚都住在安康小区,在同一所学校读书,某天早上,小强7:30从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留2分钟,校车行驶途中始终保持匀速,当天早上,小刚7:39从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早1分钟到学校站点,他们乘坐的车辆从安康小区站出发所行使路程y(千米)与行驶时间x(分钟)之间的函数图象如图所示. 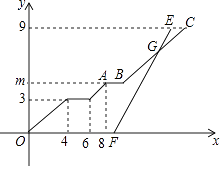
(1)求点A的纵坐标m的值;
(2)小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车?并求此时他们距学校站点的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组  请结合题意,完成本题的解答.
请结合题意,完成本题的解答.
(1)解不等式①,得 , 依据是: .
(2)解不等式③,得 .
(3)把不等式①,②和③的解集在数轴上表示出来. ![]()
(4)从图中可以找出三个不等式解集的公共部分,得不等式组的解集 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=120°,AB=10cm,点P是这个菱形内部或边上的一点.若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为cm. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( ) 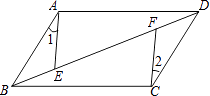
A.BE=DF
B.BF=DE
C.AE=CF
D.∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N. 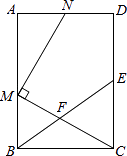
(1)当F为BE中点时,求证:AM=CE;
(2)若 ![]() =2,求
=2,求 ![]() 的值;
的值;
(3)若 ![]() =n,当n为何值时,MN∥BE?
=n,当n为何值时,MN∥BE?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,F是正方形ABCD的边CD上的一个动点,BF的垂直平分线交对角线AC于点E,连接BE,FE,则∠EBF的度数是( ) 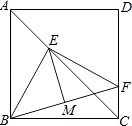
A.45°
B.50°
C.60°
D.不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com