
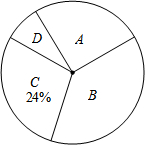
 近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,
近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,| 类别 | A | B | C | D |
| 频数 | 30 | 40 | 24 | b |
| 频率 | a | 0.4 | 0.24 | 0.06 |
分析 (1)根据B类频数和频率求出总数,再根据频数、频率、总数之间的关系分布进行计算即可;
(2)用类别为B的学生数所占的百分比乘以360°,即可得出答案;
(3)用1000乘以类别为C的人数所占的百分比,即可求出该校学生中类别为C的人数.
解答 解:(1)问卷调查的总人数是:$\frac{40}{0.4}$=100(名),
a=$\frac{30}{100}$=0.3,b=100×0.06=6(名),
故答案为:0.3,6;
(2)类别为B的学生数所对应的扇形圆心角的度数是:360°×0.4=144°;
(3)根据题意得:1000×0.24=240(名).
答:该校学生中类别为C的人数约为240名.
点评 此题考查了扇形统计图和频数(率)分布表,关键是正确从扇形统计图和表中得到所用的信息.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
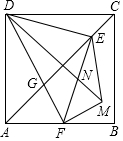 如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB边的中点,则△EMN的周长是$\frac{{5\sqrt{2}+\sqrt{10}}}{2}$.
如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB边的中点,则△EMN的周长是$\frac{{5\sqrt{2}+\sqrt{10}}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | -1 | 0 | 1 | 3 |
| y | -3 | 1 | 3 | 1 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
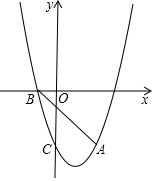 如图,抛物线y=ax2+bx-3经过点A(2,-3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
如图,抛物线y=ax2+bx-3经过点A(2,-3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x2+4x2=7x4 | B. | 2x3•3x3=6x3 | C. | a÷a-2=a3 | D. | (-$\frac{1}{2}$a2b)3=-$\frac{1}{6}$a6b3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com