
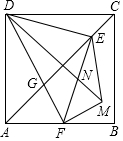
 如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB边的中点,则△EMN的周长是$\frac{{5\sqrt{2}+\sqrt{10}}}{2}$.
如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB边的中点,则△EMN的周长是$\frac{{5\sqrt{2}+\sqrt{10}}}{2}$. 分析 解法一:如图1,作辅助线,构建全等三角形,根据全等三角形对应边相等证明FQ=BQ=PE=1,△DEF是等腰直角三角形,利用勾理计算DE=EF=$\sqrt{10}$,PD=$\sqrt{D{E}^{2}-P{E}^{2}}$=3,如图2,由平行相似证明△DGC∽△FGA,列比例式可得FG和CG的长,从而得EG的长,根据△GHF是等腰直角三角形,得GH和FH的长,利用DE∥GM证明△DEN∽△MNH,则$\frac{DE}{MH}=\frac{EN}{NH}$,得EN=$\frac{\sqrt{10}}{2}$,从而计算出△EMN各边的长,相加可得周长.
解法二,将解法一中用相似得出的FG和CG的长,利用面积法计算得出,其它解法相同.
解法三:作辅助线构建正方形和全等三角形,设EP=x,则DQ=4-x=FP=x-2,求x的值得到PF=1,AE的长;由△DGC和△FGA相似,求AG和GE的长;证△GHF和△FKM全等,所以GH=FK=4/3,HF=MK=2/3,ML=AK=10/3,DL=AD-MK=10/3,即DL=LM,所以DM在正方形对角线DB上,设NI=y,列比例式可得NI的长,分别求MN和EN的长,相加可得结论.
解答 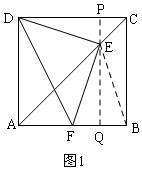 解:解法一:如图1,过E作PQ⊥DC,交DC于P,交AB于Q,连接BE,
解:解法一:如图1,过E作PQ⊥DC,交DC于P,交AB于Q,连接BE,
∵DC∥AB,
∴PQ⊥AB,
∵四边形ABCD是正方形,
∴∠ACD=45°,
∴△PEC是等腰直角三角形,
∴PE=PC,
设PC=x,则PE=x,PD=4-x,EQ=4-x,
∴PD=EQ,
∵∠DPE=∠EQF=90°,∠PED=∠EFQ,
∴△DPE≌△EQF,
∴DE=EF,
∵DE⊥EF,
∴△DEF是等腰直角三角形,
易证明△DEC≌△BEC,
∴DE=BE,
∴EF=BE,
∵EQ⊥FB,
∴FQ=BQ=$\frac{1}{2}$BF,
∵AB=4,F是AB的中点,
∴BF=2,
∴FQ=BQ=PE=1,
∴CE=$\sqrt{2}$,PD=4-1=3,
Rt△DAF中,DF=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
DE=EF=$\sqrt{10}$,
如图2,∵DC∥AB,
∴△DGC∽△FGA,
∴$\frac{CG}{AG}=\frac{DC}{AF}=\frac{DG}{FG}$=$\frac{4}{2}$=2,
∴CG=2AG,DG=2FG,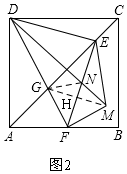
∴FG=$\frac{1}{3}$×$2\sqrt{5}$=$\frac{2\sqrt{5}}{3}$,
∵AC=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
∴CG=$\frac{2}{3}$×$4\sqrt{2}$=$\frac{8\sqrt{2}}{3}$,
∴EG=$\frac{8\sqrt{2}}{3}$-$\sqrt{2}$=$\frac{5\sqrt{2}}{3}$,
连接GM、GN,交EF于H,
∵∠GFE=45°,
∴△GHF是等腰直角三角形,
∴GH=FH=$\frac{\frac{2\sqrt{5}}{3}}{\sqrt{2}}$=$\frac{\sqrt{10}}{3}$,
∴EH=EF-FH=$\sqrt{10}$-$\frac{\sqrt{10}}{3}$=$\frac{2\sqrt{10}}{3}$,
由折叠得:GM⊥EF,MH=GH=$\frac{\sqrt{10}}{3}$,
∴∠EHM=∠DEF=90°,
∴DE∥HM,
∴△DEN∽△MNH,
∴$\frac{DE}{MH}=\frac{EN}{NH}$,
∴$\frac{\sqrt{10}}{\frac{\sqrt{10}}{3}}$=$\frac{EN}{NH}$=3,
∴EN=3NH,
∵EN+NH═EH=$\frac{2\sqrt{10}}{3}$,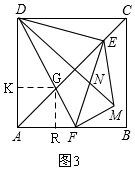
∴EN=$\frac{\sqrt{10}}{2}$,
∴NH=EH-EN=$\frac{2\sqrt{10}}{3}$-$\frac{\sqrt{10}}{2}$=$\frac{\sqrt{10}}{6}$,
Rt△GNH中,GN=$\sqrt{G{H}^{2}+N{H}^{2}}$=$\sqrt{(\frac{\sqrt{10}}{3})^{2}+(\frac{\sqrt{10}}{6})^{2}}$=$\frac{5\sqrt{2}}{6}$,
由折叠得:MN=GN,EM=EG,
∴△EMN的周长=EN+MN+EM=$\frac{\sqrt{10}}{2}$+$\frac{5\sqrt{2}}{6}$+$\frac{5\sqrt{2}}{3}$=$\frac{5\sqrt{2}+\sqrt{10}}{2}$;
解法二:如图3,过G作GK⊥AD于K,作GR⊥AB于R,
∵AC平分∠DAB,
∴GK=GR,
∴$\frac{{S}_{△ADG}}{{S}_{△AGF}}$=$\frac{\frac{1}{2}AD•KG}{\frac{1}{2}AF•GR}$=$\frac{AD}{AF}$=$\frac{4}{2}$=2,
∵$\frac{{S}_{△ADG}}{{S}_{△AGF}}$=$\frac{\frac{1}{2}DG•h}{\frac{1}{2}GF•h}$=2,
∴$\frac{DG}{GF}=2$,
同理,$\frac{{S}_{△DNF}}{{S}_{△MNF}}$=$\frac{DF}{FM}=\frac{DN}{MN}$=3,
其它解法同解法一,
可得:∴△EMN的周长=EN+MN+EM=$\frac{\sqrt{10}}{2}$+$\frac{5\sqrt{2}}{6}$+$\frac{5\sqrt{2}}{3}$=$\frac{5\sqrt{2}+\sqrt{10}}{2}$;
解法三:如图4,过E作EP⊥AP,EQ⊥AD,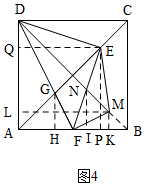
∵AC是对角线,
∴EP=EQ,
易证△DQE和△FPE全等,
∴DE=EF,DQ=FP,且AP=EP,
设EP=x,则DQ=4-x=FP=x-2,
解得x=3,所以PF=1,
∴AE=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∵DC∥AB,
∴△DGC∽△FGA,
∴同解法一得:CG=$\frac{2}{3}$×$4\sqrt{2}$=$\frac{8\sqrt{2}}{3}$,
∴EG=$\frac{8\sqrt{2}}{3}$-$\sqrt{2}$=$\frac{5\sqrt{2}}{3}$,
AG=$\frac{1}{3}$AC=$\frac{4\sqrt{2}}{3}$,
过G作GH⊥AB,过M作MK⊥AB,过M作ML⊥AD,
则易证△GHF≌△FKM全等,
∴GH=FK=$\frac{4}{3}$,HF=MK=$\frac{2}{3}$,
∵ML=AK=AF+FK=2+$\frac{4}{3}$=$\frac{10}{3}$,DL=AD-MK=4-$\frac{2}{3}$=$\frac{10}{3}$,
即DL=LM,
∴∠LDM=45°
∴DM在正方形对角线DB上,
过N作NI⊥AB,则NI=IB,
设NI=y,
∵NI∥EP
∴$\frac{NI}{EP}=\frac{FI}{FP}$
∴$\frac{y}{3}=\frac{2-y}{1}$,
解得y=1.5,
所以FI=2-y=0.5,
∴I为FP的中点,
∴N是EF的中点,
∴EN=0.5EF=$\frac{\sqrt{10}}{2}$,
∵△BIN是等腰直角三角形,且BI=NI=1.5,
∴BN=$\frac{3}{2}\sqrt{2}$,BK=AB-AK=4-$\frac{10}{3}$=$\frac{2}{3}$,BM=$\frac{2}{3}\sqrt{2}$,MN=BN-BM=$\frac{3}{2}\sqrt{2}$-$\frac{2}{3}\sqrt{2}$=$\frac{5}{6}\sqrt{2}$,
∴△EMN的周长=EN+MN+EM=$\frac{\sqrt{10}}{2}$+$\frac{5\sqrt{2}}{6}$+$\frac{5\sqrt{2}}{3}$=$\frac{5\sqrt{2}+\sqrt{10}}{2}$;
故答案为:$\frac{{5\sqrt{2}+\sqrt{10}}}{2}$.
点评 本题考查了正方形的性质、翻折变换的性质、三角形全等、相似的性质和判定、勾股定理,三角函数,计算比较复杂,作辅助线,构建全等三角形,计算出PE的长是关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
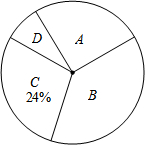 近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,
近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,| 类别 | A | B | C | D |
| 频数 | 30 | 40 | 24 | b |
| 频率 | a | 0.4 | 0.24 | 0.06 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
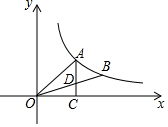 如图,A、B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若D为OB的中点,△ADO的面积为3,则k的值为8.
如图,A、B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若D为OB的中点,△ADO的面积为3,则k的值为8.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
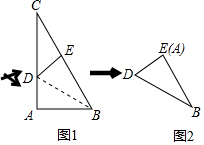 在三角形纸片ABC中,∠A=90°,∠C=30°,AC=30cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),减去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为40或$\frac{80\sqrt{3}}{3}$cm.
在三角形纸片ABC中,∠A=90°,∠C=30°,AC=30cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),减去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为40或$\frac{80\sqrt{3}}{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
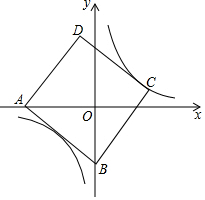 如图,正方形ABCD的边长为5,点A的坐标为(-4,0),点B在y轴上,若反比例函数y=$\frac{k}{x}$(k≠0)的图象过点C,则该反比例函数的表达式为( )
如图,正方形ABCD的边长为5,点A的坐标为(-4,0),点B在y轴上,若反比例函数y=$\frac{k}{x}$(k≠0)的图象过点C,则该反比例函数的表达式为( )| A. | y=$\frac{3}{x}$ | B. | y=$\frac{4}{x}$ | C. | y=$\frac{5}{x}$ | D. | y=$\frac{6}{x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com