
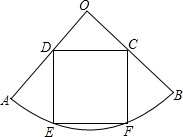
 如图,扇形AOB的圆心角∠AOB=90°,半径为5,正方形CDEF内接于该扇形,则正方形CDEF的边长为
如图,扇形AOB的圆心角∠AOB=90°,半径为5,正方形CDEF内接于该扇形,则正方形CDEF的边长为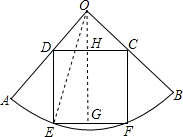 解:过O作OG⊥EF,交CD于点H,连接OE,
解:过O作OG⊥EF,交CD于点H,连接OE,
| ||
| 2 |
| 10 |
| 10 |
| 10 |


科目:初中数学 来源: 题型:
| 5 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.汽车到达乙地时油箱中还余油
张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.汽车到达乙地时油箱中还余油查看答案和解析>>
科目:初中数学 来源: 题型:
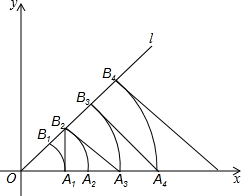 如图,已知直线l的表达式为y=x,点A1的坐标为(1,0),以O为圆心,OA1为半径画弧,与直线l交于点B1,过点A1作x轴的垂线交直线l于点B2,以O为圆心,OB2为半径画弧,交x轴于A2;过点B2作直线l的垂线交x轴于点A3,以O为圆心,OA3为半径画弧,交直线l于B3;过点B3作直线,的垂线交x轴于点A4,以O为圆心,OA4为半径画弧,交直线l于B4,过点B4作直线l的垂线交x轴于点A5…按照这样规律进行下去,点B2014的坐标为
如图,已知直线l的表达式为y=x,点A1的坐标为(1,0),以O为圆心,OA1为半径画弧,与直线l交于点B1,过点A1作x轴的垂线交直线l于点B2,以O为圆心,OB2为半径画弧,交x轴于A2;过点B2作直线l的垂线交x轴于点A3,以O为圆心,OA3为半径画弧,交直线l于B3;过点B3作直线,的垂线交x轴于点A4,以O为圆心,OA4为半径画弧,交直线l于B4,过点B4作直线l的垂线交x轴于点A5…按照这样规律进行下去,点B2014的坐标为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com