
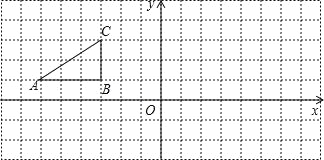
【题目】如图,方格纸中的每个小方格都是正方形,△ABC的顶点均在格点上,建立平面直角坐标系.
(1)以原点O为对称中心,画出与△ABC关于原点O对称的△A1B1C1,A1的坐标是 .
(2)将原来的△ABC绕着点(﹣2,1)顺时针旋转90°得到△A2B2C2,试在图上画出△A2B2C2的图形.
 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】手机微信推出了抢红包游戏,它有多种玩法,其中一种为“拼手气红包”,用户设定好总金额以及红包个数后,可以生成不等金额的红包.现有一用户发了三个“拼手气红包”,总金额为3元,随机被甲、乙、丙三人抢到.
(1)判断下列事件中,哪些是确定事件,哪些是不确定事件?
①丙抢到金额为1元的红包;
②乙抢到金额为4元的红包
③甲、乙两人抢到的红包金额之和一定比丙抢到的红包金额多;
(2)记金额最多、居中、最少的红包分别为A,B,C.
①求出甲抢到红包A的概率;
②若甲没抢到红包A,则乙能抢到红包A的概率又是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年3月份,某市深陷“十面霾伏”,一周空气质量报告中某项污染指数是:231,235,231,234,230,231,225,则这组数据的中位数,众数分别是( )
A.232,231
B.231,232
C.231,231
D.232,235
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机微信推出了抢红包游戏,它有多种玩法,其中一种为“拼手气红包”,用户设定好总金额以及红包个数后,可以生成不等金额的红包.现有一用户发了三个“拼手气红包”,总金额为3元,随机被甲、乙、丙三人抢到.
(1)判断下列事件中,哪些是确定事件,哪些是不确定事件?
①丙抢到金额为1元的红包;
②乙抢到金额为4元的红包
③甲、乙两人抢到的红包金额之和一定比丙抢到的红包金额多;
(2)记金额最多、居中、最少的红包分别为A,B,C.
①求出甲抢到红包A的概率;
②若甲没抢到红包A,则乙能抢到红包A的概率又是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.

(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com