
设抛物线y=ax2+bx+c(a≠0)过A(0,2),B(4,3),C三点,其中点C在直线x=2上,且点C到抛物线的对称轴的距离等于1,则抛物线的函数解析式为
科目:初中数学 来源: 题型:
如图,已知直角坐标平面上的△ABC,AC=CB,∠ACB=90°,且A(﹣1,0),B(m,n),C(3,0).若抛物线y=ax2+bx﹣3经过A、C两点.
(1)求a、b的值;
(2)将抛物线向上平移若干个单 位得到的新抛物线恰好经过点B,求新抛物线的解析式;
位得到的新抛物线恰好经过点B,求新抛物线的解析式;
(3)设(2)中的新抛物的顶点P点,Q为新抛物线上P点至B点之间的一点,以点Q为圆心画图,当⊙Q与x轴和直线BC都相切时,联结PQ、BQ,求四边形ABQP的面积.
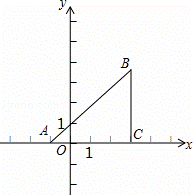
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,二次函y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=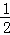 ,且经过点(2,0),下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(﹣2,y1),(
,且经过点(2,0),下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(﹣2,y1),(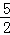 ,y2)是抛物线上的两点,则y1<y2,其中说法正确的是( )
,y2)是抛物线上的两点,则y1<y2,其中说法正确的是( )
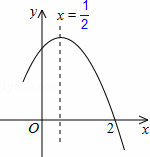
A. ①②④ B③④ C.①③④ D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
在2014年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套.设销售单价为x(x≥60)元,销售量为y套.
(1)求出y与x的函数关系式.
(2)当销售单价为多少元时,月销售额为14000元;
(3)当销售单价为多少元时,才能在一个月内获得最大利润?最大利润是多少?
[参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是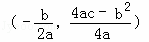 ].
].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com