
【题目】在抗击新冠状病毒战斗中,有152箱公共卫生防护用品要运到![]() 、
、![]() 两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往
两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往![]() 、
、![]() 两城镇的运费分别为每辆800元和900元,用小货车运往
两城镇的运费分别为每辆800元和900元,用小货车运往![]() 、
、![]() 两城镇的运费分别为每辆400元和600元.
两城镇的运费分别为每辆400元和600元.
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往![]() 城镇,其余货车前往
城镇,其余货车前往![]() 城镇,设前往
城镇,设前往![]() 城镇的大货车为
城镇的大货车为![]() 辆,前往
辆,前往![]() 、
、![]() 两城镇总费用为
两城镇总费用为![]() 元,试求出
元,试求出![]() 与
与![]() 的函数解析式.若运往
的函数解析式.若运往![]() 城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.
城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.
【答案】(1) 大货车用8辆,小货车用7辆;(2) ![]() 与
与![]() 的函数解析式为y=100x+9400;当运往
的函数解析式为y=100x+9400;当运往![]() 城镇的防护用品不能少于100箱,最低费用为9900元.
城镇的防护用品不能少于100箱,最低费用为9900元.
【解析】
(1)设大货车用x辆,小货车用y辆,然后根据题意列出二元一次方程组并求解即可;
(2)设前往A城镇的大货车为x辆,则前往B城镇的大货车为(8-x)辆,前往A城镇的小货车为(10-x)辆,前往B城镇的小货车为[7-(10-x)]辆,然后根据题意即可确定y与x的函数关系式;再结合已知条件确定x的取值范围,求出总费用的最小值即可.
解:(1)设大货车用x辆,小货车用y辆,根据题意得:
![]()
解得:![]()
答:大货车用8辆,小货车用7辆;
(2)设前往A城镇的大货车为x辆,则前往B城镇的大货车为(8-x)辆,前往A城镇的小货车为(10-x)辆,前往B城镇的小货车为[7-(10-x)]辆,
根据题意得:y=800x+900(8-x)+400(10-x)+600[7-(10-x)]=100x+9400
由运往![]() 城镇的防护用品不能少于100箱,则12x+ 8 (10-x)≥100,解得x≥5且x为整数;
城镇的防护用品不能少于100箱,则12x+ 8 (10-x)≥100,解得x≥5且x为整数;
当x=5时,费用最低,则:100×5+9400=9900元.
答:![]() 与
与![]() 的函数解析式为y=100x+9400;当运往
的函数解析式为y=100x+9400;当运往![]() 城镇的防护用品不能少于100箱,最低费用为9900元.
城镇的防护用品不能少于100箱,最低费用为9900元.


科目:初中数学 来源: 题型:
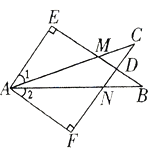
【题目】如图,在△ABE和△ACF中,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF.下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中,正确的是_________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
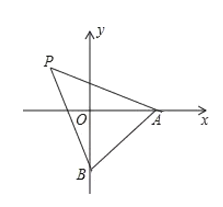
【题目】如图1,已知点![]() ,
,![]() 、
、![]() 分别交
分别交![]() 轴正半轴于点
轴正半轴于点![]() ,交
,交![]() 轴负半轴于点
轴负半轴于点![]() ,且
,且![]() ,连接
,连接![]() .
.
(1)若![]() ,则
,则![]() _______,此时
_______,此时![]() ________.
________.
(2)求![]() 的面积.
的面积.
(3)在线段![]() 上取一点
上取一点![]() 使
使![]() ,在
,在![]() 上是否存在一点
上是否存在一点![]() ,使得四边形
,使得四边形![]() 是平行四边形,如果存在,请直接写出点
是平行四边形,如果存在,请直接写出点![]() 的横坐标,如果不存在,请说明理由.
的横坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
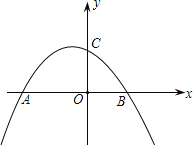
【题目】如图,抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C
(1)求点A、B的坐标;
(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;
(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE=∠BDF,点M在线段DF上,∠ABE=∠DBM.

(1)如图1,当∠ABC=45°时,求证:AE=![]() MD;
MD;
(2)如图2,当∠ABC=60°时,
①直接写出线段AE,MD之间的数量关系;
②延长BM到P,使MP=BM,连接CP,若AB=7,AE=![]() ,探求sin∠PCB的值.
,探求sin∠PCB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
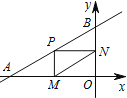
【题目】如图,直线![]() 与x轴、y轴分别交于A、B两点,点P是第二象限图象上一动点,PM⊥x轴于点M,PN⊥y轴于点N,连接MN,在点P的运动过程中,线段MN长度的最小值是________.
与x轴、y轴分别交于A、B两点,点P是第二象限图象上一动点,PM⊥x轴于点M,PN⊥y轴于点N,连接MN,在点P的运动过程中,线段MN长度的最小值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
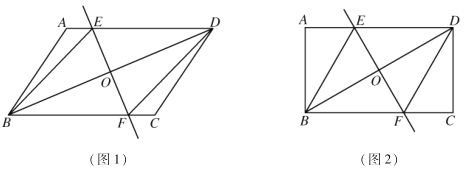
【题目】已知:在![]() 中,作对角线
中,作对角线![]() 的垂直平分线
的垂直平分线![]() ,垂足为点
,垂足为点![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图1,求证:四边形![]() 是菱形;
是菱形;
(2)如图2,当![]() ,且
,且![]() 时,在不添加任何辅助线情况下,请直接写出图2中的四条线段,使写出的每条线段长度都等于
时,在不添加任何辅助线情况下,请直接写出图2中的四条线段,使写出的每条线段长度都等于![]() 长度的
长度的![]() 倍.
倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学现有的五个社团:![]() .文学,
.文学,![]() .辩论,
.辩论,![]() .体育,
.体育,![]() .奥数,
.奥数,![]() .围棋,为了选出“你最喜爱的社团”,在部分同学中开展了调查( 每名被调查的同学必须且只能选出一个社团),并将调查结果进行了统计,绘制了如下两幅不完整的统计图:
.围棋,为了选出“你最喜爱的社团”,在部分同学中开展了调查( 每名被调查的同学必须且只能选出一个社团),并将调查结果进行了统计,绘制了如下两幅不完整的统计图:
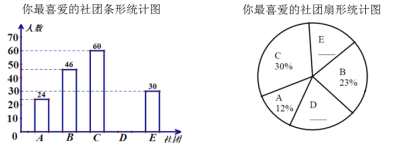
![]() 求本次被调查的人数;
求本次被调查的人数;
![]() 将上面两幅统计图补充完整;
将上面两幅统计图补充完整;
![]() 若该学校大约有学生
若该学校大约有学生![]() 人,请你估计喜欢体育社团的人数;
人,请你估计喜欢体育社团的人数;
![]() 学校为社团安排了
学校为社团安排了![]() 号教室供社团活动使用,文学设社和辩论社使用的教室恰好相邻的概率是多少?
号教室供社团活动使用,文学设社和辩论社使用的教室恰好相邻的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com