
解:(1)∵M(0,

)在y=

x+b上,
∴

=

×0+b,
∴b=

;
(2)由(1)得:y=

x+

,
∵B
1(1,y
1)在l上,
∴当x=1时,
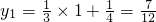
,
∴
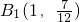
.
解法一:
∴设抛物线表达式为:y=a(x-1)
2+

(a≠0),
又∵x
1=d,
∴A
1(d,0),
∴0=a(d-1)
2+

,
∴a=-
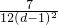
,
∴经过点A
1、B
1、A
2的抛物线的解析式为:
y=-
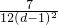
(x-1)
2+

.
解法二:
∵x
1=d,
∴A
1(d,0),A
2(2-d,0),
∴设y=a(x-d)•(x-2+d)(a≠0),
把
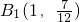
代入:

=a(1-d)•(1-2+d),
得

,
∴抛物线的解析式为y=-
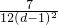
(x-d)•(x-2+d);
(3)存在美丽抛物线.
由抛物线的对称性可知,所构成的直角三角形必是以抛物线顶点为直角顶点的等腰直角三角形,
∴此等腰直角三角形斜边上的高等于斜边的一半,
又∵0<d<1,
∴等腰直角三角形斜边的长小于2,
∴等腰直角三角形斜边上的高必小于1,即抛物线的顶点的纵坐标必小于1.
∵当x=1时,
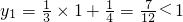
,
当x=2时,
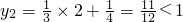
,
当x=3时,
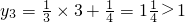
,
∴美丽抛物线的顶点只有B
1、B
2.
①若B
1为顶点,由
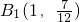
,则
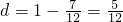
;
②若B
2为顶点,由
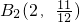
,则

,
综上所述,d的值为

或

时,存在美丽抛物线.
分析:(1)把(0,

)代入y=

x+b中,可求出b的值;
(2)由(1)可得函数解析式,y=

x+

,把(1,y
1)代入一次函数式,可求出y
1,根据图象可知,经过A
1、B
1、A
2的二次函数的顶点就是B
1,故其对称轴就是x=1,那么可设函数解析式为:y=a(x-1)
2+

,再把A
1的值代入函数式,可求出a的值,那么就可得到二次函数的解析式;
(3)存在.根据抛物线的对称性,可知所得直角三角形必是等腰直角三角形,斜边上的高等于斜边的一半,再由d的取值范围,可知斜边小于2,再把x=1,x=2,x=3…代入一次函数中,可求出相应y的值,看哪些小于1,即是所求,然后再求出d的相应数值.
点评:本题主要考查了利用了二次函数的对称性,以及等腰直角三角形的性质,要结合图形进行分析.

 x+b,经过点M(0,
x+b,经过点M(0, ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).
),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).
 解:(1)∵M(0,
解:(1)∵M(0, )在y=
)在y= x+b上,
x+b上, =
= ×0+b,
×0+b, ;
; x+
x+ ,
,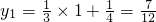 ,
,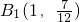 .
. (a≠0),
(a≠0), ,
,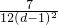 ,
,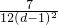 (x-1)2+
(x-1)2+ .
.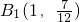 代入:
代入: =a(1-d)•(1-2+d),
=a(1-d)•(1-2+d), ,
,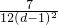 (x-d)•(x-2+d);
(x-d)•(x-2+d);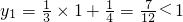 ,
,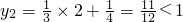 ,
,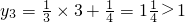 ,
,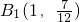 ,则
,则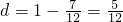 ;
;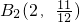 ,则
,则 ,
, 或
或 时,存在美丽抛物线.
时,存在美丽抛物线. )代入y=
)代入y= x+b中,可求出b的值;
x+b中,可求出b的值; x+
x+ ,把(1,y1)代入一次函数式,可求出y1,根据图象可知,经过A1、B1、A2的二次函数的顶点就是B1,故其对称轴就是x=1,那么可设函数解析式为:y=a(x-1)2+
,把(1,y1)代入一次函数式,可求出y1,根据图象可知,经过A1、B1、A2的二次函数的顶点就是B1,故其对称轴就是x=1,那么可设函数解析式为:y=a(x-1)2+ ,再把A1的值代入函数式,可求出a的值,那么就可得到二次函数的解析式;
,再把A1的值代入函数式,可求出a的值,那么就可得到二次函数的解析式;

 原点O及A、B两点.
原点O及A、B两点. 交于点G,垂足分别是E、F,AC是⊙O的弦,
交于点G,垂足分别是E、F,AC是⊙O的弦, 已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=
已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=