Question

△ABC中，已知sinA=cosB，则△ABC必是    三角形．

Answer 1

【答案】分析：分为两种情况：①当∠A和∠B都是锐角时，根据锐角三角函数的概念，一个角的正弦值等于它的余角的余弦值．②当∠A和∠B一个锐角、一个钝角时，举特殊例子求出是等腰三角形．
解答：解：①当∠A和∠B都是锐角时，
∵sinA=cosB，
∴∠A和∠B互余．
则△ABC是直角三角形；
②当∠A和∠B一个锐角、一个钝角时，
如设∠A=120°，sinA=
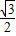
∠B=30°，cosB=，
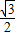
∴∠C═180°-120°-30°=30°
∴∠C=∠B，
∴△ABC是等腰三角形，
故答案为：等腰或直角．
点评：掌握互为余角的正余弦关系：一个角的正弦值等于它的余角的余弦值注意要进行分类讨论啊．