
 如图,四边形ABCD为⊙O的内接四边形,且对角线AC为直径,AD=BC,过点D作DG⊥AC,垂足为E,DG分别与AB及CB延长线交于点F、M.
如图,四边形ABCD为⊙O的内接四边形,且对角线AC为直径,AD=BC,过点D作DG⊥AC,垂足为E,DG分别与AB及CB延长线交于点F、M.分析 (1)由直径所对的圆周角等于90°可知∠ADC=∠ABC=90°,然后利用HL可证明Rt△ADC≌Rt△CBA,依据全等三角形的性质得到∠CAD=∠ACB,然后令平行线的判定定理可得到AD∥BC,依据有一组对边平行且相等的四边形为平行四边形可知ABCD是平行四边形,然后由∠ABC=90°,可证明四边形ABCD是矩形.
(2)连接OB.依据直角三角形斜边上中线的性质可得到GF=GB,则∠GBF=∠GFB=∠AFE,由OA=OB,可证明∠OBA=∠OAB,由∠AFE+∠OAB=90°,可得到∠GBF+∠OBA=90°;
(3)先证明△ACD∽△DMC,由相似三角形对应边成比例可求得DC=6,最后利用矩形的面积=长×宽求解即可.
解答 解:(1)∵AC是⊙O的直径,
∴∠ADC=∠ABC=90°.
在Rt△ADC和Rt△CBA中,AC=CA,AD=CB,
∴Rt△ADC≌Rt△CBA,
∴∠CAD=∠ACB,
∴AD∥BC,
又∵AD=BC,
∴四边形ABCD是平行四边形.
又∵∠ABC=90°,
∴□ABCD是矩形.
(2)证明:连接OB.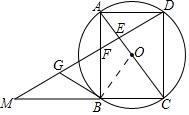
在Rt△MBF中,G是MF的中点,
∴BG=$\frac{1}{2}$MF=FG,
∴∠GBF=∠GFB=∠AFE.
∵OA=OB,
∴∠OBA=∠OAB.
∵DG⊥AC,
∴∠AFE+∠OAB=90°,
∴∠GBF+∠OBA=90°,即OB⊥BG,
∴BG是⊙O的切线.
(3)由(1)得四边形ABCD是矩形,
∴∠ADC=∠DCM=90°.
又∵AC⊥DG,
∴∠CDM+∠ACD=90°,∠CDM+∠M=90°
∴∠ACD=∠M.
又∵∠ADC=∠DCM,
∴△ACD∽△DMC,
∴$\frac{AD}{DC}=\frac{DC}{CM}$,
∴DC2=AD•CM=36,
∴DC=6,
∴S矩形ABCD=AD•CD=24.
点评 本题主要考查的是圆的综合应用,解答本题主要应用了相似三角形的性质、切线的性质和判定、矩形的性质、全等三角形的性质和判定,能够灵活应用相关知识是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | A款女鞋销量 | B款女鞋销量 | 销售总额 |
| 6月1日 | 12双 | 8双 | 2240元 |
| 6月2日 | 8双 | 10双 | 1960元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
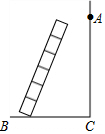 如图,墙A处需要维修,A处距离墙脚C处12米,墙下是一条宽BC为5米的小河,现要架一架梯子维修A处的墙体,现有一架14米长的梯子,问这架梯子能否到达墙的A处?
如图,墙A处需要维修,A处距离墙脚C处12米,墙下是一条宽BC为5米的小河,现要架一架梯子维修A处的墙体,现有一架14米长的梯子,问这架梯子能否到达墙的A处?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,长方体底面是长为2cm 宽为1cm的长方形,其高为8cm.
如图,长方体底面是长为2cm 宽为1cm的长方形,其高为8cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com